
【題目】如圖![]() 中,
中,![]() ,P是斜邊AC上一個動點,以即為直徑作
,P是斜邊AC上一個動點,以即為直徑作![]() 交BC于點D,與AC的另一個交點E,連接DE.
交BC于點D,與AC的另一個交點E,連接DE.
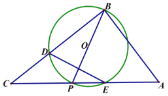
(1)當![]() 時,
時,
①若![]() ,求
,求![]() 的度數;
的度數;
②求證![]() ;
;
(2)當![]() ,
,![]() 時,
時,
①是含存在點P,使得![]() 是等腰三角形,若存在求出所有符合條件的CP的長;
是等腰三角形,若存在求出所有符合條件的CP的長;
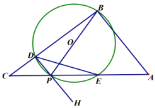
②以D為端點過P作射線DH,作點O關于DE的對稱點Q恰好落在![]() 內,則CP的取值范圍為________.(直接寫出結果)
內,則CP的取值范圍為________.(直接寫出結果)
【答案】(1)①40°;②詳見解析;(2)①7,10,12.5;②![]()
【解析】
(1)①由BP是直徑可得![]() ,根據
,根據![]() 得
得 ![]() 并可得
并可得![]() ,
, ![]() ,
,![]() ,根據三角形的內角和定理得
,根據三角形的內角和定理得![]() ;②由
;②由![]() ,得到
,得到![]() ,根據
,根據![]() ,
,![]() ,
,![]() ,得到,
,得到,![]() 由等角對等邊得
由等角對等邊得![]() ;
;
(2)①分三種情況:(一)當![]() 時,(二)當
時,(二)當![]() 時,(三)當
時,(三)當![]() 時,分別進行討論求解即可;
時,分別進行討論求解即可;
②分三種情況討論:(一)當Q點在P點上時;(二)當Q點在PC上時(三)當Q點在PH上時,分別討論,求出CP的值即可.
24.解(1)①連結BE,∵BP是直徑∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ∴
∴![]()
∴![]()
②∵![]() ,∴
,∴![]()
![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
(2)①由![]() ,
,![]() ,可以求得
,可以求得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]()
當![]() 是等腰三角形時,有三種情況:(一)
是等腰三角形時,有三種情況:(一)![]() ,(二)
,(二)![]() ,(三)
,(三)![]()
(一)當![]() 時,
時,![]()
∴![]() ,
,
∴![]()
∴![]()
(二)當![]() 時,可知點D是
時,可知點D是![]() 斜邊的中線,
斜邊的中線,
∴![]() ,
,
∴![]()
∴![]()
(三)當![]() 時,
時,
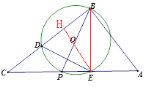
作![]() ,則H是BD中點,
,則H是BD中點,
可以求得![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
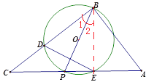
②(一)當O點的對稱點Q在P點上時,B,O,Q三點共線,
如圖示
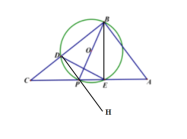
∴![]() ,且BP平分DE,由等腰三角形的性質可知
,且BP平分DE,由等腰三角形的性質可知
∴![]()
由(1)可知CP=7;
(二)當O點的對稱點Q不在P點上,而在PC上時,此情況Q點并不在![]() 上
上
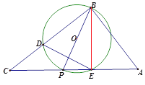
(三)當O點的對稱點Q不在P點上,而在PH上時,B,O,Q三點不共線,
如圖示
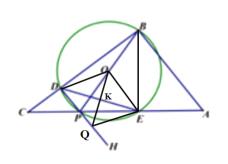
∵![]() ,
,![]() ,且
,且![]()
∴四邊形DOEQ是菱形,
∴![]()
∵![]()
∴![]()
又∵OE,OD,OB均為外接圓的半徑,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴由(1)可知,![]()
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
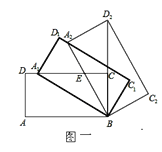
【題目】如圖一,矩形ABCD中,AB=m,BC=n,將此矩形繞點B順時針方向旋轉θ(0°<θ<90°)得到矩形A1BC1D1,點A1在邊CD上.
(1)若m=2,n=1,求在旋轉過程中,點D到點D1所經過路徑的長度;
(2)將矩形A1BC1D1繼續繞點B順時針方向旋轉得到矩形A2BC2D2,點D2在BC的延長線上,設邊A2B與CD交于點E,若![]() ,求
,求![]() 的值.
的值.
(3)如圖二,在(2)的條件下,直線AB上有一點P,BP=2,點E是直線DC上一動點,在BE左側作矩形BEFG且始終保持![]() ,設AB=
,設AB=![]() ,試探究點E移動過程中,PF是否存在最小值,若存在,求出這個最小值;若不存在,請說明理由.
,試探究點E移動過程中,PF是否存在最小值,若存在,求出這個最小值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“早黑寶”葡萄品種是我省農科院研制的優質新品種,在我省被廣泛種植,鄧州市某葡萄種植基地2017年種植“早黑寶”100畝,到2019年“卓黑寶”的種植面積達到196畝.
(1)求該基地這兩年“早黑寶”種植面積的平均增長率;
(2)市場調查發現,當“早黑寶”的售價為20元/千克時,每天能售出200千克,售價每降價1元,每天可多售出50千克,為了推廣宣傳,基地決定降價促銷,同時減少庫存,已知該基地“早黑寶”的平均成本價為12元/千克,若使銷售“早黑寶”每天獲利1750元,則售價應降低多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解中學生對《最強大腦》、《朗讀者》、《中國詩詞大會》、《出彩中國人》四個電視節目的喜愛情況,隨機抽取了![]() 名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如圖統計圖表:
名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如圖統計圖表:
節目 | 人數(名) | 百分比 |
最強大腦 |
|
|
朗讀者 |
|
|
中國詩詞大會 |
|
|
出彩中國人 |
|
|
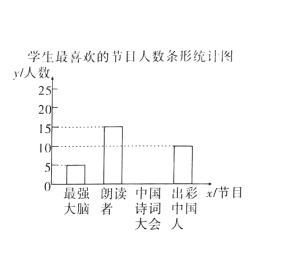
根據以上提供的信息.解答下列問題:
![]() ,
,![]() ,
,![]() ;
;
![]() 補全上面的條形統計圖;
補全上面的條形統計圖;
![]() 名女同學.其余為男同學,現要從中隨機抽取
名女同學.其余為男同學,現要從中隨機抽取![]() 名同學代表學校參加市里組織的競賽活動,請求出所抽取的
名同學代表學校參加市里組織的競賽活動,請求出所抽取的![]() 名同學恰好是
名同學恰好是![]() 名男同學和
名男同學和![]() 名女同學的概率.
名女同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是作一個角的角平分線的方法:以![]() 的頂點
的頂點![]() 為圓心,以任意長為半徑畫弧,分別交
為圓心,以任意長為半徑畫弧,分別交![]() 于
于![]() 兩點,再分別以
兩點,再分別以![]() 為圓心,大于
為圓心,大于![]() 長為半徑作畫弧,兩條弧交于點
長為半徑作畫弧,兩條弧交于點![]() ,作射線
,作射線![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .
.

(1)若![]() ,求
,求![]() 的度數;
的度數;
(2)若![]() ,垂足為
,垂足為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩所醫院分別有一男一女共4名醫護人員支援湖北武漢抗擊疫情.
(1)若從甲、乙兩醫院支援的醫護人員中分別隨機選1名,則所選的2名醫護人員性別相同的概率是 ;
(2)若從支援的4名醫護人員中隨機選2名,用列表或畫樹狀圖的方法求出這2名醫護人員來自同一所醫院的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學社團成員想利用所學的知識測量某廣告牌的寬度![]() 圖中線段MN的長
圖中線段MN的長![]() ,直線MN垂直于地面,垂足為點
,直線MN垂直于地面,垂足為點![]() 在地面A處測得點M的仰角為
在地面A處測得點M的仰角為![]() 、點N的仰角為
、點N的仰角為![]() ,在B處測得點M的仰角為
,在B處測得點M的仰角為![]() ,
,![]() 米,且A、B、P三點在一直線上
米,且A、B、P三點在一直線上![]() 請根據以上數據求廣告牌的寬MN的長.
請根據以上數據求廣告牌的寬MN的長.
![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 三個頂點的坐標分別為
三個頂點的坐標分別為![]() ,
,![]() ,
,![]()
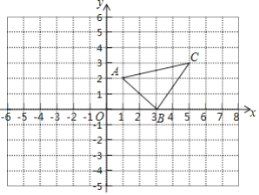
(1)請畫出![]() 向下平移5個單位長度后得到的
向下平移5個單位長度后得到的![]() ;
;
(2)請畫出![]() 關于
關于![]() 軸對稱的
軸對稱的![]() ;
;
(3)若坐標軸上存在點![]() ,使得
,使得![]() 是以
是以![]() 為底邊的等腰三角形,請直接寫出滿足條件的點
為底邊的等腰三角形,請直接寫出滿足條件的點![]() 坐標.
坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com