
【題目】(1)問題發(fā)現(xiàn)
如圖![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() , 連接
, 連接![]() ,
,![]() 交于點
交于點![]() .填空:①
.填空:①![]() 的值為 :②
的值為 :②![]() 的度數(shù)為
的度數(shù)為
(2)類比探究
如圖![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() , 連接
, 連接![]() 交
交![]() 的延長線于點
的延長線于點![]() .請求出
.請求出![]() 能的值及
能的值及![]() 的度數(shù), 并說明理由;
的度數(shù), 并說明理由;
(3)拓展延伸
在![]() 的條件下, 將
的條件下, 將![]() 繞點
繞點![]() 在平面內旋轉,
在平面內旋轉,![]() 所在直線交于點
所在直線交于點![]() , 若
, 若![]() ,
,![]() ,請直接寫出當點
,請直接寫出當點![]() 與點
與點![]() 重合時
重合時![]() 的長.
的長.

【答案】(1)![]() ;
;![]() (2)
(2)![]() .理由見解析(3)
.理由見解析(3)![]() 的長為
的長為![]() 或
或![]() .
.
【解析】
(1)①證明![]() ,得到AC=BD,比值為1;②由
,得到AC=BD,比值為1;②由![]() 得
得![]() ,根據(jù)三角形內角和定理得,
,根據(jù)三角形內角和定理得,![]() =
=![]() .
.
(2)根據(jù)兩邊的比相等且夾角相等可得![]() ∽
∽![]() ,則
,則![]() ,由全等三角形的性質得
,由全等三角形的性質得![]() 的度數(shù).
的度數(shù).
(3)正確畫出圖形,當點C與點M重合時,有兩種情況:如圖3和如圖4,同理可得![]() ,則
,則![]() ,
,![]() ,可得AC的長.
,可得AC的長.
(1)![]() ;
;![]()
①如圖1.
∵![]() ,
,
∴![]() ,
,
∵OC=OD,OA=OB,
∴![]() ,
,
∴AC=BD,
∴![]() .
.
②∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() ,
,
![]() ,
,
=![]() ,
,
=![]() ,
,
故答案為:1,![]() .
.
(2)![]() .理由如下:
.理由如下:
在![]() ,中
,中![]()
∴![]() ,同理可得
,同理可得![]()
∴![]()
∵![]()
∴![]()
∴![]() ∽
∽![]()
∴![]()
![]()
∴![]()
(3)拓展延伸
①點C與點M重合時,如圖3,同理得:![]() ,
,
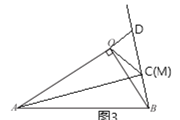
∴![]() ,
,![]() ,
,
設![]() ,則
,則![]() ,
,
Rt△COD中,![]() ,OD=1,
,OD=1,
∴![]() ,
,![]() ,
,
Rt△AOB中,![]() ,
,![]() ,
,
∴![]() ,
,
在RtAMB中,由勾股定理得:
![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ;
;
②點C與點M重合時,如圖4,
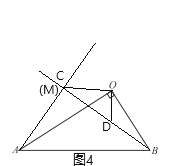
同理得:![]() ,
,![]() ,
,
設![]() ,則
,則![]() ,
,
在RtAMB中,由勾股定理得:
![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]()
綜上所述:![]() 的長為
的長為![]() 或
或![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】某公司生產的一種產品按照質量由高到低分為A,B,C,D四級,為了增加產量、提高質量,該公司改進了一次生產工藝,使得生產總量增加了一倍.為了解新生產工藝的效果,對改進生產工藝前、后的四級產品的占比情況進行了統(tǒng)計,繪制了如下扇形圖:
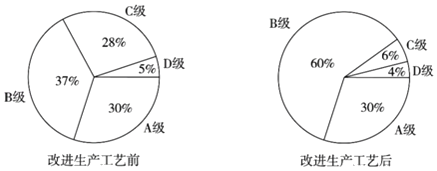
根據(jù)以上信息,下列推斷合理的是( )
A.改進生產工藝后,A級產品的數(shù)量沒有變化
B.改進生產工藝后,B級產品的數(shù)量增加了不到一倍
C.改進生產工藝后,C級產品的數(shù)量減少
D.改進生產工藝后,D級產品的數(shù)量減少
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知四邊形![]() 中,
中,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 邊上的點,
邊上的點,![]() 與
與![]() 交于點
交于點![]() .
.
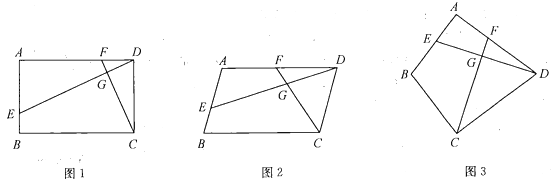
(1)如圖1,若四邊形![]() 是矩形,且
是矩形,且![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若四邊形![]() 是平行四邊形,試探究:當
是平行四邊形,試探究:當![]() 與
與![]() 滿足什么關系時,使得
滿足什么關系時,使得![]() 成立?并證明你的結論;
成立?并證明你的結論;
(3)如圖3,若![]() ,
,![]() ,
,![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小麗早晨6:00從家里出發(fā),騎車去菜場買菜,然后從菜場返回家中.小麗離家的路程![]() (米)和所經過的時間
(米)和所經過的時間![]() (分)之間的函數(shù)圖象如圖所示,請根據(jù)圖象回答下列問題:
(分)之間的函數(shù)圖象如圖所示,請根據(jù)圖象回答下列問題:

(1)小麗去菜場途中的速度是多少?在菜場逗留了多長時間?
(2)小麗幾點幾分返回到家?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
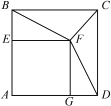
【題目】如圖,正方形AEFG的頂點E、G在正方形ABCD的邊AB、AD上,連接BF、DF.
![]() (1)求證:BF=DF;
(1)求證:BF=DF;
(2)連接CF,請直接寫出![]() 的值為__________(不必寫出計算過程).
的值為__________(不必寫出計算過程).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我校八年級有800名學生,在體育中考前進行一次排球模擬測試,從中隨機抽取部分學生,根據(jù)其測試成績制作了下面兩個統(tǒng)計圖,請根據(jù)相關信息,解答下列問題:

(1)本次抽取到的學生人數(shù)為________,圖2中![]() 的值為_________.
的值為_________.
(2)本次調查獲取的樣本數(shù)據(jù)的平均數(shù)是__________,眾數(shù)是________,中位數(shù)是_________.
(3)根據(jù)樣本數(shù)據(jù),估計我校八年級模擬體測中得12分的學生約有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
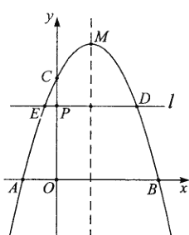
【題目】如圖,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,
,![]() (點
(點![]() 位于對稱軸的左側),與
位于對稱軸的左側),與![]() 軸交于點
軸交于點![]() .點
.點![]() 為線段
為線段![]() 上一點,過點
上一點,過點![]() 作直線
作直線![]() 軸交圖象于點
軸交圖象于點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的左側),且
的左側),且![]() .
.
(1)求該二次函數(shù)的對稱軸及![]() 的值.
的值.
(2)將頂點![]() 向右平移
向右平移![]() 個單位至點
個單位至點![]() ,再過點
,再過點![]() 作直線
作直線![]() 的對稱點
的對稱點![]() ,若點
,若點![]() 在
在![]() 軸上方的圖象上一點且到
軸上方的圖象上一點且到![]() 軸距離為1,求
軸距離為1,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
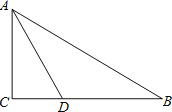
【題目】已知:如圖,在![]() 中,
中,![]() 的角平分線
的角平分線![]() 交
交![]() 邊于
邊于![]() .
.
(1)以![]() 邊上一點
邊上一點![]() 為圓心,過
為圓心,過![]() 兩點作
兩點作![]() (不寫作法,保留作圖痕跡),再判斷直線
(不寫作法,保留作圖痕跡),再判斷直線![]() 與
與![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)若(1)中的![]() 與
與![]() 邊的另一個交點為
邊的另一個交點為![]() ,
,![]() ,求線段
,求線段![]() 與劣弧
與劣弧![]() 所圍成的圖形面積.(結果保留根號和
所圍成的圖形面積.(結果保留根號和![]() )
)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com