【題目】當
取最小值時，代數式
的最小值為__________．
【答案】
【解析】
根據絕對值的定義可知|a+b-4|+2|b+2|的最小值為0，得出a=6，b=-2，代入代數式|x+a+b|-|x-b|計算即可．
解：∵|a+b-4|≥0 2|b+2|≥0
∴|a+b-4|+2|b+2|≥0
∴根據題意|a+b-4|+2|b+2|=0，得a=6，b=-2
把a=-2，b=-2代入|x+a+b|-|x-b|=|x+4|-|x+2|
①當x≥-2時，|x+4|-|x+2|=x+4-（x+2）=2
②當-4＜x＜-2時，|x+4|-|x+2|=x+4-（-x-2）=2x+6
∵-4＜x＜-2，-2＜2x+6＜2
③當x≤-4時，|x+4|-|x+2|=-x-4-（-x-2）=-2
綜上所述，|x+a+b|-|x-b|的最小值為-2．
故答案為-2．
科目：初中數學 來源： 題型：
【題目】問題再現：
數形結合是一種重要的數學思想方法，借助這種思想方法可將抽象的數學知識變得直觀并且具有可操作性.初中數學里的一些代數公式，很多都可以通過表示幾何圖形面積的方法進行直觀推導和解釋.
例如：利用圖形的幾何意義驗證完全平方公式.
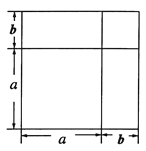
將一個邊長為
的正方形的邊長增加
，形成兩個長方形和兩個正方形，如圖所示：這個圖形的面積可以表示成：
或
∴
這就驗證了兩數和的完全平方公式.
類比解決：
請你類比上述方法，利用圖形的幾何意義驗證平方差公式.
（要求畫出圖形并寫出推理過程）
問題提出：如何利用圖形幾何意義的方法證明
？
如圖所示，
表示1個1×1的正方形，即：
，
表示1個2×2的正方形，
與
恰好可以拼成1個2×2的正方形，因此：、、就可以表示2個2×2的正方形，即：
而、、、恰好可以拼成一個
的大正方形.
由此可得：
.
嘗試解決：
請你類比上述推導過程，利用圖形的幾何意義確定：
_______.（要求寫出結論并構造圖形寫出推證過程）.
問題拓廣：
請用上面的表示幾何圖形面積的方法探究：
_______.（直接寫出結論即可，不必寫出解題過程）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E．
（1）若∠BAC=50°，求∠EDA的度數；
（2）求證：直線AD是線段CE的垂直平分線．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一輛貨車從百貨大樓出發送貨，向東走了4千米到達小明家，繼續向東走了1.5千米到達小紅家，然后向西走了8.5千米到達小剛家，最后返回百貨大樓．
（1）以百貨大樓為原點，向東為正方向，1個單位長度表示1千米，請在數軸上標出小明、小紅、小剛家的位置．（小明家用點
表示，小紅家用點
表示，小剛家用點
表示）
（2）求這輛貨車此次送貨（從出發到返回百貨大樓）總共走的路程．
查看答案和解析>>
科目：初中數學 來源： 題型：
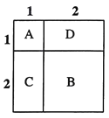
【題目】將四張邊長各不相同的正方形紙片按如圖方式放入矩形
內(相鄰紙片之間互不重疊也無縫隙)，未被四張正方形紙片覆蓋的部分用陰影表示．設右上角與左下角陰影部分的周長的差為
．若知道的值，則不需測量就能知道周長的正方形的標號為（ ）
A.①B.②C.③D.④
查看答案和解析>>
科目：初中數學 來源： 題型：
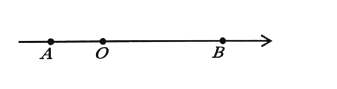
【題目】如圖，在數軸上點
表示的數為
，點
表示的數為
，且
滿足
，
為原點．若動點
從點出發，以每秒
個單位長度的速度沿數軸向右勻速運動，設運動的時間為
(秒) ．
求的值；
當點運動到線段
上時，分別取和
的中點
，試探究下列結論:
①
的值為定值；②
的值為定值，
其中有且只有一個是正確的，請將正確的選出來并求出該值；
當點從點出發運動到點時，另一動點
從點出發，以每秒
個單位長度的速度在間往返運動，當
時，求動點運動的時間的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小亮從家出發步行到公交站臺后,等公交車去學校,如圖, 折線表示這個過程中行程 s （千米）與所花時間 t （分）之間的關系,下 列說法錯誤的是（ ）
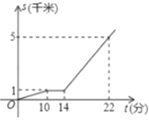
A.他家到公交車站臺需行 1 千米B.他等公交車的時間為 4 分鐘
C.公交車的速度是 500 米/分D.他步行與乘公交車行駛的平均速度300米/分鐘
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的頂點P是BC邊上的中點，兩邊PE，PF分別交AB，AC于點E，F，給出以下四個結論：
①AE=CF；②EF=AP；③2S四邊形AEPF=S△ABC；④當∠EPF在△ABC內繞頂點P旋轉時（點E不與A，B重合）有BE+CF=EF；上述結論中始終正確的序號有__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
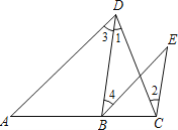
【題目】已知：如圖，∠1=∠2，∠3=∠E，試說明：∠A=∠EBC，（請按圖填空，并補理由，）
證明：∵∠1=∠2（已知），
∴______∥______，________
∴∠E=∠______，________
又∵∠E=∠3（已知），
∴∠3=∠______（等量代換），
∴______∥______（內錯角相等，兩直線平行），
∴∠A=∠EBC，________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com