
【題目】已知,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分線
的垂直平分線![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,垂足為
,垂足為![]() .
.
(1)如圖,連接![]() 、
、![]() .求證四邊形
.求證四邊形![]() 為菱形,并求
為菱形,并求![]() 的長;
的長;
(2)如圖,動點![]() 、
、![]() 分別從
分別從![]() 、
、![]() 兩點同時出發,沿
兩點同時出發,沿![]() 和
和![]() 各邊勻速運動一周.即點
各邊勻速運動一周.即點![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止,點
停止,點![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止.在運動過程中,
停止.在運動過程中,
①已知點![]() 的速度為每秒5
的速度為每秒5![]() ,點
,點![]() 的速度為每秒4
的速度為每秒4![]() ,運動時間為
,運動時間為![]() 秒,當
秒,當![]() 、
、![]() 、
、![]() 、
、![]() 四點為頂點的四邊形是平行四邊形時,求
四點為頂點的四邊形是平行四邊形時,求![]() 的值.
的值.
②若點![]() 、
、![]() 的運動路程分別為
的運動路程分別為![]() 、
、![]() (單位:
(單位:![]() ,
,![]() ),已知
),已知![]() 、
、![]() 、
、![]() 、
、![]() 四點為頂點的四邊形是平行四邊形,寫出
四點為頂點的四邊形是平行四邊形,寫出![]() 與
與![]() 滿足的數量關系式.(直接寫出答案,不要求證明)
滿足的數量關系式.(直接寫出答案,不要求證明)

【答案】(1)證明略,![]() (2) ①
(2) ①![]() 秒. ②
秒. ②![]() 與
與![]() 滿足的函數關系式是
滿足的函數關系式是![]()
【解析】
試題(1)先證明四邊形AFCE為平行四邊形,再根據對角線互相垂直平分的平行四邊形是菱形作出判定;根據勾股定理即可求得AF的長;
(2)分情況討論可知,當P點在BF上、Q點在ED上時,才能構成平行四邊形,根據平行四邊形的性質列出方程求解即可.
試題解析:(1)證明:①∵四邊形![]() 是矩形
是矩形
∴![]() ∥
∥![]()
∴![]() ,
,![]()
∵![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]()
∴![]()
∴![]() ≌
≌![]()
∴![]()
∴四邊形![]() 為平行四邊形
為平行四邊形
又∵![]()
∴四邊形![]() 為菱形
為菱形
②設菱形的邊長![]() ,則
,則![]()
在![]() 中,
中,![]()
解得![]()
∴![]()
(2)①顯然當![]() 點在
點在![]() 上時,
上時,![]() 點在
點在![]() 上,此時
上,此時![]() 、
、![]() 、
、![]() 、
、![]() 四點不可能構成平行四邊形;同理
四點不可能構成平行四邊形;同理![]() 點在
點在![]() 上時,
上時,![]() 點在
點在![]() 或
或![]() 上,也不能構成平行四邊形.因此只有當
上,也不能構成平行四邊形.因此只有當![]() 點在
點在![]() 上、
上、![]() 點在
點在![]() 上時,才能構成平行四邊形
上時,才能構成平行四邊形
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四點為頂點的四邊形是平行四邊形時,
四點為頂點的四邊形是平行四邊形時,![]()
∵點![]() 的速度為每秒10cm,點
的速度為每秒10cm,點![]() 的速度為每秒6cm,運動時間為
的速度為每秒6cm,運動時間為![]() 秒
秒
∴![]() ,
,
∴![]() ,解得
,解得![]()
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四點為頂點的四邊形是平行四邊形時,
四點為頂點的四邊形是平行四邊形時,![]() 秒.
秒.
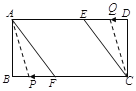
②由題意得,以![]() 、
、![]() 、
、![]() 、
、![]() 四點為頂點的四邊形是平行四邊形時,點
四點為頂點的四邊形是平行四邊形時,點![]() 、
、![]() 在互相平行的對應邊上.
在互相平行的對應邊上.
分三種情況:
i)如圖1,當![]() 點在
點在![]() 上、
上、![]() 點在
點在![]() 上時,
上時,![]() ,
,![]() ,即
,即![]()
ii)如圖2,當![]() 點在
點在![]() 上、
上、![]() 點在
點在![]() 上時,
上時,![]() ,
,![]() ,即
,即![]()
iii)如圖3,當![]() 點在
點在![]() 上、
上、![]() 點在
點在![]() 上時,
上時,![]() ,
,![]() ,即
,即![]()
綜上所述,![]() 與
與![]() 滿足的函數關系式是
滿足的函數關系式是![]()


 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是平行四邊形,下列結論中不正確的是( )

A. 當AB=BC時,它是菱形 B. 當AC⊥BD時,它是菱形
C. 當∠ABC=90°時,它是矩形 D. 當AC=BD時,它是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點O是AC邊上的一個動點,過點O作直線MN∥BC,設MN交∠BCA的角平分線于點E,交∠BCA的外角平分線于點F.
(1)求證:EO=FO;
(2)當點O運動到何處時,四邊形AECF是矩形?并證明你的結論.
(3)當點O運動到何處,且△ABC滿足什么條件時,四邊形AECF是正方形?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班舉行了“慶祝建黨98周年知識競賽”活動,班長安排張小明購買獎品,如圖兩幅圖是張小明買回獎品時與班長的對話情況:

請根據圖1、圖2的信息,解答下列問題:
(1)張小明買了兩種筆記本各多少本?(要求列一元一次方程解決問題)
(2)為什么班長說不可能找回68元錢,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在方格紙中
(1)請在方格紙上建立平面直角坐標系,使A(2,3),C(6,2),并求出B點坐標;
(2)以原點O為位似中心,相似比為2,在第一象限內將△ABC放大,畫出放大后的圖形△A′B′C′;
(3)計算△A′B′C′的面積S.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家2002年四個季度的用電量如下:
季度名稱 | 用電量(單位:千瓦時) |
第一季度 | 250 |
第二季度 | 150 |
第三季度 | 400 |
第四季度 | 200 |
其中各種電器用電量如下表:
各種電器 | 用電量(單位:千瓦時) |
空調 | 250 |
冰箱 | 400 |
照明 | 100 |
彩電 | 150 |
其他 | 100 |
小明根據上面的數據制成下面的統計圖.
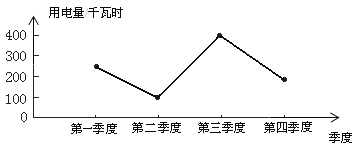
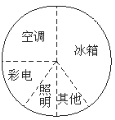
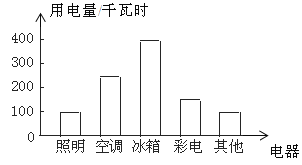
根據以上三幅統計圖回答:
(1)從哪幅統計圖中可以看出各個季度用電量變化情況?
(2)從哪幅統計圖中可以看出冰箱用電量超過總用電量的![]() ?
?
(3)從哪幅統計圖中可以清楚地看出空調的用電量?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com