【題目】根據完全平方公式可以作如下推導（a、b都為非負數）
∵ a-2
+b=(
-
)2≥0 ∴ a-2+b≥0
∴ a+b≥2 ∴ 
≥
其實，這個不等關系可以推廣，
≥
… …
（以上an都是非負數）
我們把這種關系稱為：算術—幾何均值不等式
例如：x為非負數時，
，則
有最小值．
再如：x為非負數時，x+x+
．
我們來研究函數：
（1）這個函數的自變量x的取值范圍是 ；
（2）完成表格并在坐標系中畫出這個函數的大致圖象；
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
（3）根據算術—幾何均值不等式，該函數在第一象限有最 值，是 ；
（4）某同學在研究這個函數時提出這樣一個結論：當x>a時，y隨x增大而增大,則a的取值范圍是 ．
【答案】⑴ x≠0；⑵ -1，3，詳見解析；⑶ 小，3 ；⑷ a≥1
【解析】
（1）根據分式的分母不能為0即可得；
（2）分別將
和代入函數的解析式可求出對應的y的值，再利用描點法畫出這個函數的大致圖象即可；
（3）根據算術—幾何均值不等式求解即可得；
（4）根據（2）所畫出的函數圖象得出y隨x增大而增大時，x的取值范圍，由此即可得出答案．
（1）由分式的分母不能為0得：函數
的自變量x的取值范圍是
故答案為：；
（2）對于函數
當時，
當時，
因此，補全表格如下：
x | … |
|
|
|
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
|
| 3 | 5 |
| … |
利用描點法畫出這個函數的大致圖象如下：
（3）函數在第一象限時，
由算術—幾何均值不等式得：
則
有最小值，最小值為3
故答案為：小，3；
（4）由（2）的函數圖象可知，當
時，y隨x增大而增大
則a的取值范圍是
故答案為：．
科目：初中數學 來源： 題型：
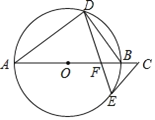
【題目】如圖，AB是⊙O的直徑，點D，E在⊙O上，∠A=2∠BDE，點C在AB的延長線上，∠C=∠ABD．
（1）求證：CE是⊙O的切線；
（2）若⊙O的半徑長為5，BF=2，求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A.了解一批燈泡的使用壽命采用全面調查
B.一組數據6，5，3，5，4的眾數是5，中位數是3
C.“367人中必有2人的生日是同一天”是必然事件
D.一組數據10，11，12，9，8的平均數是10，方差是1.5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
與
軸交于
、
兩點（在的左側），與
軸交于點
，過點的直線
：
與軸交于點
，與拋物線的另一個交點為
，己知
，
，
點為拋物線上一動點（不與、重合）．
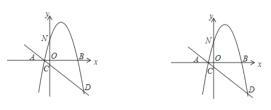
（1）直接寫出拋物線和直線的解析式；
（2）當點在直線上方的拋物線上時，連接
、
，
①當
的面積最大時，點的坐標是________；
②當
平分
時，求線段的長．
（3）設
為直線上的點，探究是否存在點，使得以點、，、為頂點的四邊形為平行四邊形？若存在，直接寫出點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，拋物線
（
是常數，且
）與
軸交于
、
兩點（點在點的左邊），與
軸交于點
．連結
，將線段繞點順時針旋轉
，得到線段
，連結
．當最短時，的值為_________ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知函數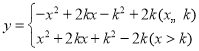
，（
為常數）．
（1）當
時，
①求此函數圖象與
軸交點坐標．
②當函數的值隨
的增大而增大時，自變量的取值范圍為________．
（2）若已知函數經過點（1，5），求的值，并直接寫出當
時函數的取值范圍．
（3）要使已知函數的取值范圍內同時含有
和
這四個值，直接寫出的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
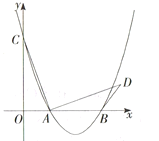
【題目】如圖，已知二次函數
（
）的圖象與x軸交于點A（﹣1，0），對稱軸為直線x=1，與y軸的交點B在（0，2）和（0，3）之間（包括這兩點），下列結論：
①當x＞3時，y＜0；
②3a+b＜0；
③
；
④
；
其中正確的結論是（ ）
A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
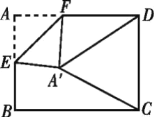
【題目】如圖，在矩形紙片
中，
，
，點
是
的中點，點
是
邊上的一個動點，將
沿
所在直線翻折，得到
，連接
，
，則當
是以為腰的等腰三角形時，
的長是___________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
