
【題目】某公司為了了解員工每人所創年利潤情況,公司從各部抽取部分員工對每年所創利潤進行統計,并繪制如圖1,圖2統計圖.
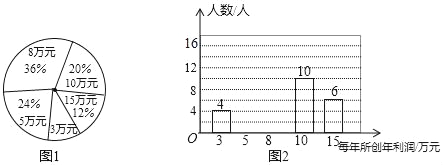
(1)將圖2補充完整;
(2)本次共抽取員工 人,每人所創年利潤的眾數是 萬元,平均數是 萬元,中位數是 萬元;
(3)若每人創造年利潤10萬元及(含10萬元)以上為優秀員工,在公司1200員工中有多少可以評為優秀員工?
【答案】(1)補圖見解析;(2)50;8;8.12;8;(3)384
【解析】試題分析:(1)根據扇形統計圖計算3萬元的員工的百分比為8%,進而結合條形統計圖得到抽取員工的總數為50人,得到5萬元的員工人數和8萬元的員工人數,據此補全統計圖;
(2)3萬元的員工的百分比為8%,人數為4人,所以抽取員工總數為:4÷8%=50人,每人所創年利潤的眾數即出現次數最多的數8萬元,利用求平均數的公式求平均數;
(3)先計算每人創造年利潤10萬元及(含10萬元)以上的比例,然后計算1200員工中有多少人達到優秀.
試題解析:解:(1)3萬元的員工的百分比為:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取員工總數為:4÷8%=50(人),
5萬元的員工人數為:50×24%=12(人),
8萬元的員工人數為:50×36%=18(人),
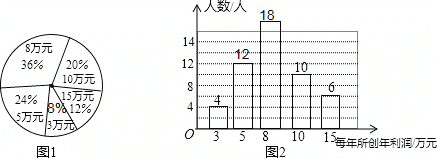
(2)抽取員工總數為:4÷8%=50(人),
每人所創年利潤的眾數是 8萬元,
平均數是:![]() ×(3×4+5×12+8×18+10×10+15×6)=8.12萬元.
×(3×4+5×12+8×18+10×10+15×6)=8.12萬元.
故答案為:50;8萬元;8.12萬元.
(3)1200×![]() =384(人),
=384(人),
答:在公司1200員工中有384人可以評為優秀員工.


科目:初中數學 來源: 題型:
【題目】某市區自2014年1月起,居民生活用水開始實行階梯式計量水價,該階梯式計量水價分為三級(如下表所示):
月用水量(噸) | 水價(元/噸) |
第一級 20噸以下(含20噸) | 1.6 |
第二級 20噸﹣30噸(含30噸) | 2.4 |
第三級 30噸以上 | 3.2 |
例:某用戶的月用水量為32噸,按三級計量應繳水費為:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用戶的月用水量為12噸,則甲需繳的水費為 元;
(2)如果乙用戶繳的水費為39.2元,則乙月用水量 噸;
(3)如果丙用戶的月用水量為a噸,則丙用戶該月應繳水費多少元?(用含a的代數式表示,并化簡)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠現有甲種原料360千克,乙種原料290千克,計劃利用這兩種原料生產A、B兩種產品共50件,已知生產一件A種產品用甲種原料9千克,乙種原料3千克,可獲利700元;生產一件B種產品用甲種原料4千克,乙種原料10千克,可獲利1200元.
(1)按要求安排A、B兩種產品的生產件數,有哪幾種方案?請你設計出來;
(2)設生產A、B兩種產品總利潤為y元,其中一種產品生產件數為x件,試寫出y與x之間的函數關系式,并利用函數的性質說明那種方案獲利最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】多肉植物是指植物營養器官肥大的植物,又稱肉質植物或多肉花卉,由于體積小、外形萌、色彩斑斕,茶幾陽臺擺放方便,近年來越來越受到廣大養花愛好者的喜愛.多肉植物則被親切地稱為“肉肉”、“多肉君”.大學畢業生陳江河發現這個商機后,第一次果斷購進甲乙兩種多肉植物共500株.甲種多肉植物每株成本5元,售價10元;乙種多肉植物每株成本8元,售價10元.
(1)由于啟動資金有限,第一次購進多肉植物的金額不得超過3400元,則甲種多肉植物至少購進多少株?
(2)多肉植物一經上市,十分搶手,陳江河決定第二次購進甲乙兩種多肉植物,它們的進價不變.甲種多肉植物進貨量在(1)的最少進貨量的基礎上增加了![]() ,售價也提高了
,售價也提高了![]() ;乙種多肉植物的售價和進貨量不變,但是由于乙種多肉植物的耐熱性不強,導致銷售完之前它的成活率為
;乙種多肉植物的售價和進貨量不變,但是由于乙種多肉植物的耐熱性不強,導致銷售完之前它的成活率為![]() .結果第二次共獲利2700元.求m的值.
.結果第二次共獲利2700元.求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店準備購進一批電冰箱和空調,每臺電冰箱的進價比每臺空調的進價多400元,商店用8000元購進電冰箱的數量與用6400元購進空調的數量相等.
(1)求每臺電冰箱與空調的進價分別是多少?
(2)已知電冰箱的銷售價為每臺2100元,空調的銷售價為每臺1750元.若商店準備購進這兩種家電共100臺,其中購進電冰箱x臺(33≤x≤40),那么該商店要獲得最大利潤應如何進貨?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列三行數:

(1)第①行的第n個數是_______(直接寫出答案,n為正整數)
(2)第②、③行的數與第①行相對應的數分別有什么關系?
(3)取每行的第9個數,記這三個數的和為a,化簡計算求值:(5a2-13a-1)-4(4-3a+![]() a2)
a2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數![]() 的圖像與一次函數
的圖像與一次函數![]() 的圖像交于點
的圖像交于點![]() ,點
,點![]() .
.
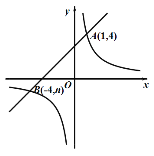
(1)求k和b的值;
(2)連接OA、OB,求![]() 的面積;
的面積;
(3)利用圖像,直接寫出![]() 時x的取值范圍.
時x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com