【題目】如圖所示，在矩形ABCD中，AB=12，AC=20，兩條對角線相交于點O．以OB、OC為鄰邊作第1個平行四邊形OBB1C，對角線相交于點A1，再以A1B1、A1C為鄰邊作第2個平行四邊形A1B1C1C，對角線相交于點O1；再以O1B1、O1C1為鄰邊作第3個平行四邊形O1B1B2C1…依此類推．
（1）求矩形ABCD的面積；
（2）求第1個平行四邊形OBB1C的面積是
第2個平行四邊形A1B1C1C是
第3個平行四邊形O1B1B2C1的面積是
（3）求第n個平行四邊形的面積是
【答案】（1）192；（2）96,48,24；（3）192×(
)n
【解析】分析：(1)用勾股定理求出BC的長；(2)由圖形可知每一個平行四邊形的面積都是它前面的平行四邊形面積的，用列舉法可得到第n個平行四邊形的面積；(3)見(2)中的解析.
詳解：
(1)解：∵四邊形ABCD是矩形，AC＝20，AB＝12
∴∠ABC＝90°，BC＝
＝
＝16.
∴S矩形ABCD＝AB·BC＝12×16＝192.
(2)第1個平行四邊形OBB1C的面積 192×＝96
第2個平行四邊形A1B1C1C是 192××＝192×()2＝48
第3個平行四邊形O1B1B2C1的面積是 192×××＝192×()3＝24
……
第n個平行四邊形的面積是 192×()n.
(3)由(2)知第n個平行四邊形的面積是192×()n.
科目：初中數學 來源： 題型：
【題目】如圖，半徑為1個單位的圓片上有一點A與數軸上的原點重合，AB是圓片的直徑．
（1）把圓片沿數軸向左滾動1周，點A到達數軸上點C的位置，點C表示的數是______數（填“無理”或“有理”），這個數是______；
（2）把圓片沿數軸滾動2周，點A到達數軸上點D的位置，點D表示的數是______；
（3）圓片在數軸上向右滾動的周數記為正數，圓片在數軸上向左滾動的周數記為負數，依次運動情況記錄如下：+2，-1，-5，+4，+3，-2當圓片結束運動時，A點運動的路程共有多少？此時點A所表示的數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，已知A（2，0），以OA為一邊在第四象限內畫正方形OABC，D（m，0）為x軸上的一個動點，以BD為一邊畫正方形BDFE（點E在直線x=2的右側）．
（1）當m>2時（如圖1），試判斷線段AE與CD的數量關系，并說明理由．
（2）當AE=
時，求點F的坐標．
（3）連接CF、OF，請直接寫出CF+OF的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠B=90°，以AB為直徑的⊙O交AC于D，過點D作⊙O的切線交BC于E，AE交⊙O于點F．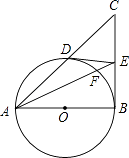 
（1）求證：E是BC的中點；
（2）求證：ADAC=AEAF=4DO2 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】蝸牛從某點
開始沿一東西方向直線爬行，規定向東爬行的路程記為正數，向西爬行的路程記為負數．爬過的各段路程依次為（單位：厘米）：
，
，
，
，
，
，
．
通過計算說明蝸牛是否回到起點
．
蝸牛離開出發點最遠時是多少厘米？
在爬行過程中，如果每爬
厘米獎勵
粒芝麻，則蝸牛一共得到多少粒芝麻？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，直線AB與x軸交于點A，與y軸交于點B，點A的坐標為（3，0），點B的坐標為（0，4），點P為雙曲線y= 
（x＞0）上的一點，過點P分別作x軸、y軸的垂線段PE、PF，當PE、PF分別與線段AB交于點C、D時，ADBC的值為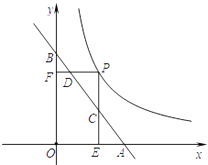
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AB＝4cm，BC＝8cm，動點M從點D出發，按折線DCBAD方向以2cm/s的速度運動，動點N從點D出發，按折線DABCD方向以1cm/s的速度運動。
（1）若動點M、N同時出發，經過幾秒鐘兩點相遇？
（2）若點E在線段BC上，且BE＝3cm，若動點M、N同時出發，相遇時停止運動，經過幾秒鐘，點A、E、M、N組成平行四邊形？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某自行車廠一周計劃生產1050輛自行車，平均每天生產150輛，由于各種原因實際每天生產量與計劃量相比有出入．下表是某周的生產情況（超產為正、減產為負）：
（1）根據記錄可知前三天共生產 輛；
（2）產量最多的一天比產量最少的一天多生產 輛；
（3）該廠實行計件工資制，每輛車50元，超額完成任務每輛獎10元，少生產一輛扣10元，那么該廠工人這一周的工資總額是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
