
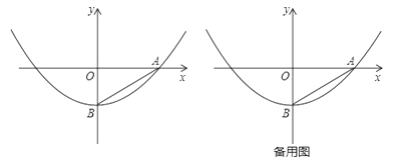
【題目】如圖,在平面直角坐標系xOy中,Rt△AOB的直角邊OA在x軸正半軸上,OB在y軸負半軸上,且OA=![]() ,OB=1,以點B為頂點的拋物線經過點A.
,OB=1,以點B為頂點的拋物線經過點A.
(1)求出該拋物線的解析式.
(2)第二象限內的點M,是經過原點且平分Rt△AOB面積的直線上一點.若OM=2,請判斷點M是否在(1)中的拋物線上?并說明理由.
(3)點P是經過點B且與坐標軸不平行的直線l上一點.請你探究:當直線l繞點B任意旋轉(不與坐標軸平行或重合)時,是否存在這樣的直線l,在直線l上能找到點P,使△PAB與Rt△AOB相似(相似比不為1)?若存在,求出直線l的解析式;若不存在,說明理由.
【答案】(1)y=![]() x2﹣1(2)點M不在拋物線y=
x2﹣1(2)點M不在拋物線y=![]() x2﹣1上(3)存在三條直線l:y=﹣
x2﹣1上(3)存在三條直線l:y=﹣![]() x﹣1,y=﹣
x﹣1,y=﹣![]() x﹣1和y=
x﹣1和y=![]() x﹣1,在上述直線l上能找到點P,使Rt△PAB與Rt△AOB相似
x﹣1,在上述直線l上能找到點P,使Rt△PAB與Rt△AOB相似
【解析】
(1)依題意得到A與B的坐標,根據B為拋物線的頂點,設出拋物線的解析式,將A坐標代入求出a的值,即可確定出拋物線解析式;
(2)點M不在拋物線上,理由為:設拋物線與x軸的另一個交點為C,直線OM交AB于點D,由題意得到D為AB的中點,得到AD=OD=BD,得到∠MON=∠AOD=∠OAD=30°,作MN垂直于OC,求出MN與ON的長,確定出M坐標,代入拋物線解析式檢驗即可得到結果;
(3)存在,在Rt△AOB中,AO=![]() ,BO=1,AB=2,∠ABO=60°,∠BAO=30°,分三種情況考慮:①當∠ABP=90°時,若∠AP1B=60°,則△ABP1∽△AOB,由相似得比例,確定出P1的坐標,再由B坐標確定出直線l解析式即可;②當∠ABP=60°時,若∠BAP5=90°,則△ABP5∽△OBA,由相似得比例求出P5坐標,同理確定出直線l解析式;③當∠ABP=30°且直線l在AB上方時,若∠P6AB=90°,則△ABP6∽△OAB,由相似得比例求出P6坐標,同理確定出直線l解析式,綜上,得到直線l上能找到點P,使Rt△PAB與Rt△AOB相似時的所有解析式.
,BO=1,AB=2,∠ABO=60°,∠BAO=30°,分三種情況考慮:①當∠ABP=90°時,若∠AP1B=60°,則△ABP1∽△AOB,由相似得比例,確定出P1的坐標,再由B坐標確定出直線l解析式即可;②當∠ABP=60°時,若∠BAP5=90°,則△ABP5∽△OBA,由相似得比例求出P5坐標,同理確定出直線l解析式;③當∠ABP=30°且直線l在AB上方時,若∠P6AB=90°,則△ABP6∽△OAB,由相似得比例求出P6坐標,同理確定出直線l解析式,綜上,得到直線l上能找到點P,使Rt△PAB與Rt△AOB相似時的所有解析式.
(1)依題意得:A(![]() ,0),B(0,﹣1),
,0),B(0,﹣1),
∵B為拋物線的頂點,
∴設拋物線解析式為y=ax2﹣1,
將A坐標代入得:3a﹣1=0,即a=![]() ,
,
則拋物線解析式為y=![]() x2﹣1;
x2﹣1;
(2)點M不在拋物線y=![]() x2﹣1上,理由為:
x2﹣1上,理由為:
設拋物線與x軸的另一個交點為C,直線OM交AB于點D,作MN⊥OC于點N,
由題意得:D為AB的中點,即OD=AD=BD,
∴∠MON=∠AOD=∠OAD=30°,
在Rt△OMN中,OM=2,
∴MN=1,ON=![]() ,即M(﹣
,即M(﹣![]() ,1),
,1),
∵y=![]() ×(﹣
×(﹣![]() )2﹣1=0≠1,
)2﹣1=0≠1,
∴點M不在拋物線y=![]() x2﹣1上;
x2﹣1上;
(3)存在,在Rt△AOB中,AO=![]() ,BO=1,AB=2,∠ABO=60°,∠BAO=30°,
,BO=1,AB=2,∠ABO=60°,∠BAO=30°,
分三種情況考慮:
①當∠ABP=90°時,若∠AP1B=60°,則△ABP1∽△AOB,
∴![]() =
=![]() ,即BP1=
,即BP1=![]() =
=![]() ,
,
∴OP1=![]() ,即P1(﹣
,即P1(﹣![]() ,0),[這里也利用求出P2(﹣
,0),[這里也利用求出P2(﹣![]() ,2)或P3(
,2)或P3(![]() ,﹣2)或P4(
,﹣2)或P4(![]() ,﹣4)],
,﹣4)],
設直線l解析式為y=kx+b,將B與P1坐標代入得: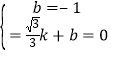 ,
,
解得:![]() ,
,
此時直線l解析式為y=﹣![]() x﹣1;
x﹣1;
②當∠ABP=60°時,若∠BAP5=90°,則△ABP5∽△OBA,
∴![]() =
=![]() ,即BP5=
,即BP5=![]() =4,
=4,
過P5作P5C⊥y軸于點G,在Rt△BGP5中,∠P5BG=60°,
∴P5G=2![]() ,BG=2,即P5(2
,BG=2,即P5(2![]() ,﹣3),
,﹣3),
同理求出直線l解析式為y=﹣![]() x﹣1;
x﹣1;
③當∠ABP=30°且直線l在AB上方時,若∠P6AB=90°,則△ABP6∽△OAB,
∴![]() =
=![]() ,即BP6=
,即BP6=![]() =
=![]() ,
,
過P6作P6H⊥y軸于點H,在Rt△BP6H中,∠P6BH=30°,
∴P6H=![]() ,BH=2,
,BH=2,
∴P6(![]() ,1),
,1),
同理得到直線l解析式為y=![]() x﹣1,
x﹣1,
綜上,存在三條直線l:y=﹣![]() x﹣1,y=﹣
x﹣1,y=﹣![]() x﹣1和y=
x﹣1和y=![]() x﹣1,在上述直線l上能找到點P,使Rt△PAB與Rt△AOB相似.
x﹣1,在上述直線l上能找到點P,使Rt△PAB與Rt△AOB相似.


科目:初中數學 來源: 題型:
【題目】有4張正面分別標有數字![]() 的不透明卡片,它們除數字不同外其余全部相同,現將它們背面朝上,洗勻后從中任取一張,將卡片上的數字記為
的不透明卡片,它們除數字不同外其余全部相同,現將它們背面朝上,洗勻后從中任取一張,將卡片上的數字記為![]() ,另有一個被均勻分成4份的轉盤,上面分別標有數字
,另有一個被均勻分成4份的轉盤,上面分別標有數字![]() ,轉動轉盤,指針所指的數字記為
,轉動轉盤,指針所指的數字記為![]() (若指針指在分割線上則重新轉一次),則點
(若指針指在分割線上則重新轉一次),則點![]() 落在拋物線
落在拋物線![]() 與
與![]() 軸所圍成的區域內(不含邊界)的概率是__________.
軸所圍成的區域內(不含邊界)的概率是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知P為![]() 所在平面內一點,連接PA,PB,PC,在
所在平面內一點,連接PA,PB,PC,在![]() ,
,![]() 和
和![]() 中,若存在一個三角形與
中,若存在一個三角形與![]() 相似
相似![]() 全等除外
全等除外![]() 那么就稱P為
那么就稱P為![]() 的共相似點”根據“共相似點“是否落在三角形的內部,邊上或外部,可將其分為內共相似點”,“邊共相似點或“外共相似點”.
的共相似點”根據“共相似點“是否落在三角形的內部,邊上或外部,可將其分為內共相似點”,“邊共相似點或“外共相似點”.
![]() 據定義可知,等邊三角形______
據定義可知,等邊三角形______![]() 填“存在”或“不存在
填“存在”或“不存在![]() 共相似點
共相似點
(探究)用邊共相似點探究三角形的形狀
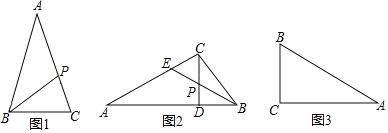
![]() 如圖1,若
如圖1,若![]() 的一個邊共相似點P與其對角項點B的連線,將
的一個邊共相似點P與其對角項點B的連線,將![]() 分割成的兩個三角形恰與原三角形均相似,試判斷
分割成的兩個三角形恰與原三角形均相似,試判斷![]() 的形狀,并說明理由.
的形狀,并說明理由.
(探究2)用內共相似點探究三角形的內角關系
![]() 如圖2,在
如圖2,在![]() 中,
中,![]() ,高線CD與角平分線BE交于點P,若P是
,高線CD與角平分線BE交于點P,若P是![]() 的一個內共相似點試說明點E是
的一個內共相似點試說明點E是![]() 的邊共相似點,并直接寫出
的邊共相似點,并直接寫出![]() 的度數;
的度數;
(探究)探究直角三角形共相似點的個數
![]() 如圖3,在
如圖3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() 與
與![]() 相以,則滿足條件的P點共有______個
相以,則滿足條件的P點共有______個![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c的頂點M在第二象限,且經過點 A(1,0)和點 B(0,2).則
(1)a 的取值范圍是________;
(2)若△AMO的面積為△ABO面積的![]() 倍時,則a的值為________
倍時,則a的值為________
查看答案和解析>>
科目:初中數學 來源: 題型:
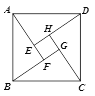
【題目】如圖是我國漢代數學家趙爽在注解《周髀算經》時給出的“趙爽弦圖”,圖中四個直角三角形是全等的,若大正方形ABCD的面積是小正方形EFGH面積的13倍,則![]() 的值為______________.
的值為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一枚運載火箭從距雷達站C處5km的地面O處發射,當火箭到達點A,B時,在雷達站C處測得點A,B的仰角分別為34°,45°,其中點O,A,B在同一條直線上.求A,B兩點間的距離(結果精確到0.1km).
(參考數據:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為進一步發展基礎教育,自2014年以來,某縣加大了教育經費的投入,2014年該縣投入教育經費6000萬元。2016年投入教育經費8640萬元。假設該縣這兩年投入教育經費的年平均增長率相同。
(1)求這兩年該縣投入教育經費的年平均增長率;
(2)若該縣教育經費的投入還將保持相同的年平均增長率,請你預算2017年該縣投入教育經費多少萬元。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com