【題目】△ABC中，∠A=30°，AC=8，∠B=90°，點D在AB上，BD=
，點P在△ABC的邊上，則當AP=2PD時，PD的長為____________________．
【答案】
或3或
【解析】
分點P在線段AB上，點P在線段AC上和點P在線段BC上三種情況求解即可.
∵∠A=30°，AC=8，∠B=90°，
∴BC=4，AB=
,
∴AD=
.
當點P在線段AB上時，如圖1，
∵AP=2PD，AP+PD=AD=3,
∴PD=;
當點P在線段AC上時，如圖2，
∵∠A=30°，
∴當PD∥BC時，AP=2PD，
∴PD:BC=AD:AB，
∴PD=
;
當點P在線段BC上時，如圖3，
∵AP2=AB2+BP2，BP2=PD2-BD2，
∴AP2=AB2+ PD2-BD2，
∴4 PD2= (4)2+ PD2-()2，
∴PD2=15,
∴PD=或PD=
（舍去）.
故答案為： 或3或.
閱讀快車系列答案科目：初中數學 來源： 題型：
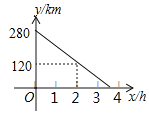
【題目】甲車從A地駛往B地，同時乙車從B地駛往A地，兩車相向而行，勻速行駛，甲車距B地的距離y（km）與行駛時間x（h）之間的函數關系如圖所示，乙車的速度是60km/h．
（1）求甲車的速度；
（2）當甲乙兩車相遇后，乙車速度變為a（km/h），并保持勻速行駛，甲車速度保持不變，結果乙車比甲車晚38分鐘到達終點，求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
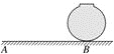
【題目】如圖是置于水平地面上的一個球形儲油罐，小敏想測量它的半徑、在陽光下，他測得球的影子的最遠點A到球罐與地面接觸點B的距離是10米(如示意圖，AB＝10米)；同一時刻，他又測得豎直立在地面上長為1米的竹竿的影子長為2米，那么，球的半徑是________米．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，△ABC的頂點坐標分別為A(－2，2)，B(－4，0)，C(－4；－4)，
（1）在y軸右側，以O為位似中心，畫出△A'B'C′，使它與△ABC的相似比為1:2；
（2）根據(1)的作圖，sin∠A'C'B′＝__________.
查看答案和解析>>
科目：初中數學 來源： 題型：
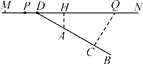
【題目】如圖，MN表示一段筆直的高架道路，線段AB表示高架道路旁的一排居民樓，已知點A到MN的距離為15米，BA的延長線與MN相交于點D，且∠BDN＝30°，假設汽車在高速道路上行駛時，周圍39米以內會受到噪音(XRS)的影響．
(1)過點A作MN的垂線，垂足為點H，如果汽車沿著從M到N的方向在MN上行駛，當汽車到達點P處時，噪音開始影響這一排的居民樓，那么此時汽車與點H的距離為多少米？
(2)降低噪音的一種方法是在高架道路旁安裝隔音板，當汽車行駛到點Q時，它與這一排居民樓的距離QC為39米，那么對于這一排居民樓，高架道路旁安裝的隔音板至少需要多少米長？(精確到1米)(參考數據：
≈1.7)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】期末考試后,某市第一中學為了解本校九年級學生期末考試數學學科成績情況,決定對該年級學生數學學科期末考試成績進行抽樣分析,已知九年級共有12個班，每班48名學生.請按要求回答下列問題：
收集數據
（1）若要從全年級學生中抽取一個96人的樣本，你認為以下抽樣方法中比較合理的有 ．(只要填寫序號即可)
①隨機抽取兩個班級的96名學生；②在全年級學生中隨機抽取96名學生；③在全年級12個班中分別各隨機抽取8名學生；④從全年級學生中隨機抽取96名男生．
整理數據
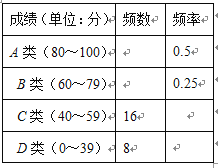
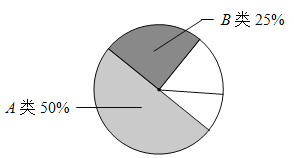
（2）將抽取的96名學生的成績進行分組，繪制頻數分布表和成績分布扇形統計圖（不完整）如下．請根據圖表中數據填空：
①C類和D類部分的圓心角度數分別為 、 ；
②估計全年級A、B類學生大約一共有 名．
分析數據
（3）學校為了解其它學校教學情況，將同層次的第一、第二兩所中學的抽樣數據進行對比，得下表：
學校 | 平均數（分） | 極差（分） | 方差 | A、B類的頻率和 |
第一中學 | 71 | 52 | 432 | 0.75 |
第二中學 | 71 | 80 | 497 | 0.82 |
你認為哪所學校的教學效果較好？結合數據，請提出一個合理解釋來支持你的觀點．
查看答案和解析>>
科目：初中數學 來源： 題型：
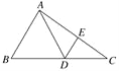
【題目】如圖，已知△ABC中，點D在邊BC上，∠DAB＝∠B，點E在邊AC上，滿足AE·CD＝AD·CE.
(1)求證：DE∥AB；
(2)如果點F是DE延長線上一點，且BD是DF和AB的比例中項，連接AF.求證：DF＝AF.
查看答案和解析>>
科目：初中數學 來源： 題型：
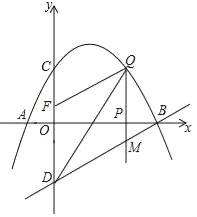
【題目】如圖，已知拋物線經過點A（﹣1，0），B（4，0），C（0，2）三點，點D與點C關于x軸對稱，點P是x軸上的一個動點，設點P的坐標為（m，0），過點P作x軸的垂線交拋物線于點Q，交直線BD于點M．
（1）求該拋物線所表示的二次函數的表達式；
（2）點P在線段AB上運動的過程中，是否存在點Q，使得△BOD∽△QBM？若存在，求出點Q的坐標；若不存在，請說明理由．
（3）已知點F（0，
），點P在x軸上運動，試求當m為何值時以D、M、Q、F為頂點的四邊形是平行四邊形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個不透明的口袋中裝有4個分別標有數1，2，3，4的小球，它們的形狀、大小完全相同，小紅先從口袋里隨機摸出一個小球記下數為x，小穎在剩下的3個球中隨機摸出一個小球記下數為y，這樣確定了點P的坐標（x，y）．
（1）小紅摸出標有數3的小球的概率是多少？．
（2）請你用列表法或畫樹狀圖法表示出由x，y確定的點P（x，y）所有可能的結果．
（3）求點P（x，y）在函數y=﹣x+5圖象上的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com