
【題目】如圖1,將1張菱形紙片ABC的(∠ADC>90°)沿對角線BD剪開,得到△ABD和△BCD.再將△BCD以D為旋轉中心,按逆時針方向旋轉角α,使α=∠ADB,得到如圖2所示的△DB′C,連接AC、BB′,∠DAB=45°,有以下結論:①AC=BB′;②AC⊥AB;③∠CDA=90°;④BB′= ![]() AB,其中正確結論的序號是 . (把所有正確結論的序號都填在橫線上)
AB,其中正確結論的序號是 . (把所有正確結論的序號都填在橫線上) 
【答案】①②③
【解析】解:如圖1, 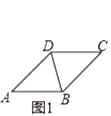
∵四邊形ABCD為菱形,
∴AB=BC=CD=AD,∠A=∠C=45°,
∴∠ADB=∠ABD=67.5°,
∴α=2∠ADB=135°,
如圖2,
∵將△BCD以D為旋轉中心,按逆時針方向旋轉角135°,
∴DB=DB′,DC=DA,CB′=AB,∠7=∠3=67.5°,∠6=135°,
在△DBB′中,∠4=∠5= ![]() (180°﹣135°)=22.5°,
(180°﹣135°)=22.5°,
∴∠ABB′=∠3+∠4=90°,∠BB′C=∠5+∠7=90°,
∴AB∥CB′,
而AB=CB′,
∴四邊形ABB′C為矩形,
∴AC=BB′,AC⊥AB,所以①②正確,
∵∠CAB=90°,∠1=45°,
∴∠CAD=45°,
而DC=DA,
∴△ADC為等腰直角三角形,
∴∠CDA=90°;BB′= ![]() AB,所以③正確,④錯誤.
AB,所以③正確,④錯誤.
所以答案是①②③.
【考點精析】根據題目的已知條件,利用菱形的性質和旋轉的性質的相關知識可以得到問題的答案,需要掌握菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半;①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】如圖,長方形![]() 中,
中,![]() =4cm,
=4cm,![]() =3cm,
=3cm,![]() 為
為![]() 的中點.動點
的中點.動點![]() 從
從![]() 點出發(fā),以每秒1cm的速度沿
點出發(fā),以每秒1cm的速度沿![]() 運動,最終到達點
運動,最終到達點![]() .若點
.若點![]() 運動的時間為
運動的時間為![]() 秒,則當
秒,則當![]() =________ 時,
=________ 時,![]() 的面積等于4.5.
的面積等于4.5.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,一次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() .
.
(1)若點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() 在一次函數
在一次函數![]() 的圖象上,求
的圖象上,求![]() 的值;
的值;
(2)求由直線![]() ,(1)中的直線
,(1)中的直線![]() 以及
以及![]() 軸圍成的三角形的面積.
軸圍成的三角形的面積.
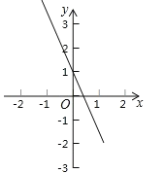
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A、C分別在x、y軸的正半軸上,點D為對角線OB的中點,點E(4,m)在邊AB上,反比例函數y= ![]() (k≠0)在第一象限內的圖象經過點D、E,且cos∠BOA=
(k≠0)在第一象限內的圖象經過點D、E,且cos∠BOA= ![]() .
.
(1)求邊AB的長;
(2)求反比例函數的解析式和m的值;
(3)若反比例函數的圖象與矩形的邊BC交于點F,點G、H分別是y軸、x軸上的點,當△OGH≌△FGH時,求線段OG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BF平分∠ABC,AF⊥BF于點F,D為AB的中點,連接DF延長交AC于點E.若AB=10,BC=18,則線段EF的長為( ) 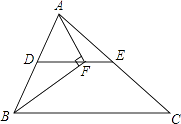
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張莊甲、乙兩家草莓采摘園的草莓銷售價格相同,“春節(jié)期間”,兩家采摘園將推出優(yōu)惠方案,甲園的優(yōu)惠方案是:游客進園需購買門票,采摘的草莓六折優(yōu)惠;乙園的優(yōu)惠方案是:游客進園不需購買門票,采摘園的草莓超過一定數量后,超過部分打折優(yōu)惠.優(yōu)惠期間,某游客的草莓采摘量為![]() (千克),在甲園所需總費用為
(千克),在甲園所需總費用為![]() (元),在乙園所需總費用為
(元),在乙園所需總費用為![]() (元),
(元),![]() 、
、![]() 與
與![]() 之間的函數關系如圖所示,折線OAB表示
之間的函數關系如圖所示,折線OAB表示![]() 與
與![]() 之間的函數關系.
之間的函數關系.

(1)甲采摘園的門票是 元,兩個采摘園優(yōu)惠前的草莓單價是每千克 元;
(2)當![]() >10時,求
>10時,求![]() 與
與![]() 的函數表達式;
的函數表達式;
(3)游客在“春節(jié)期間”采摘多少千克草莓時,甲、乙兩家采摘園的總費用相同.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,因為直線AB、CD相交于點P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因為直線a∥b,b∥c,所以a∥c(________________________________).
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等邊△ABC中,
(1)如圖1,P,Q是BC邊上兩點,AP=AQ,∠BAP=20°,求∠AQB的度數;
(2)點P,Q是BC邊上的兩個動點(不與點B,C重合),點P在點Q的左側,且AP=AQ,點Q關于直線AC的對稱點為M,連接AM,PM.
①依題意將圖2補全;②小明通過觀察、實驗,提出猜想:在點P,Q運動的過程中,始終有PA=PM,小明把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:要證PA=PM,只需證△APM是等邊三角形.
想法2:在BA上取一點N,使得BN=BP,要證PA=PM,只需證△ANP≌△PCM.……
請你參考上面的想法,幫助小明證明PA=PM(一種方法即可).
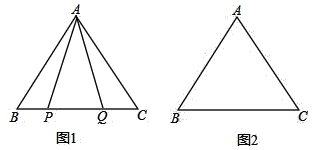
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,元旦期間,小明乘汽車從![]() 地出發(fā),經過
地出發(fā),經過![]() 地到目的地
地到目的地![]() 地(三地在同一條直線上),假設汽車從
地(三地在同一條直線上),假設汽車從![]() 到
到![]() 的過程都是勻速直線行駛.圖②表示小明離
的過程都是勻速直線行駛.圖②表示小明離![]() 地的路程
地的路程![]() (km)與汽車從
(km)與汽車從![]() 出發(fā)后行駛時間
出發(fā)后行駛時間![]() (h)之何的函數關系圖像.
(h)之何的函數關系圖像.
(1)![]() 兩地間的路程為 km;
兩地間的路程為 km;
(2)求小明離![]() 地的路程
地的路程![]() 與行駛時間
與行駛時間![]() 之間的函數表達式;
之間的函數表達式;
(3)當行駛時間![]() 在什么范圍時,汽車離
在什么范圍時,汽車離![]() 地的路程不超過40 km?
地的路程不超過40 km?

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com