
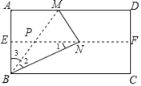
【題目】如圖,某數學興趣小組開展以下折紙活動:①對折矩形紙片ABCD,使AD和BC重合,得到折痕EF,把紙片展開;②再一次折疊紙片,使點A落在EF上,并使折痕經過點B,得到折痕BM,同時得到線段BN.觀察探究可以得到∠NBC的度數是( )

A. 20°B. 25°C. 30°D. 35°
【答案】C
【解析】
BM交EF于P,如圖,根據折疊的性質得∠BNM=∠A=90°,∠2=∠3,EF∥AD,AE=BE,則可判斷EP為△BAM的中位線,利用平行線的性質得∠1=∠NBC,根據斜邊上的中線性質得PN=PB=PM,所以∠1=∠2,從而得到∠NBC=∠2=∠3,然后利用∠NBC+∠2+∠3=90°可得到∠NBC的度數.
BM交EF于P,如圖,
∵四邊形ABCD為矩形,
∴∠A=∠ABC=90°,
∵折疊紙片,使點A落在EF上,并使折痕經過點B,得到折痕BM,同時得到線段BN,
∴∠BNM=∠A=90°,∠2=∠3,
∵對折矩形紙片ABCD,使AD和BC重合,得到折痕EF,
∴EF∥AD,AE=BE,
∴EP為△BAM的中位線,∠1=∠NBC,
∴P點為BM的中點,
∴PN=PB=PM,
∴∠1=∠2,
∴∠NBC=∠2=∠3,
∵∠NBC+∠2+∠3=90°,
∴∠NBC=30°.
故選C.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某水果公司購進10 000kg蘋果,公司想知道蘋果的損壞率,從所有蘋果中隨機抽取若干進行統計,部分結果如下表:
蘋果總質量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
損壞蘋果質量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
蘋果損壞的頻率 (結果保留小數點后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估計這批蘋果損壞的概率為_____(結果保留小數點后一位),損壞的蘋果約有______kg.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 擲一枚均勻的骰子,骰子停止轉動后,6點朝上是必然事件
B. 甲、乙兩人在相同條件下各射擊10次,他們的成績平均數相同,方差分別是S甲2=0.4,S乙2=0.6,則甲的射擊成績較穩定
C. “明天降雨的概率為![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批電視機的使用壽命,適合用普查的方式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南果梨是東北遼寧省的一大特產,現有20筐南國梨,以每筐25千克為標準,超過或不足的千克數分別用正、負數來表示,記錄如下:
與標準質量的差值 (單位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐數 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐南果梨中,最重的一筐比最輕的一筐重多少千克?
(2)與標準重量比較,20筐南果梨總計超過或不足多少千克?
(3)若南果梨每千克售價4元,則這20筐可賣多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
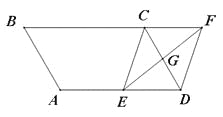
【題目】(7分)如圖,平行四邊形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中點,E是邊AD上的動點,EG的延長線與BC的延長線交于點F,連接CE,DF.
(1)求證:四邊形CEDF是平行四邊形;
(2)①當AE= cm時,四邊形CEDF是矩形;
②當AE= cm時,四邊形CEDF是菱形;(直接寫出答案,不需要說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(閱讀理解)對于任意正實數a、b,
∵(![]() ﹣
﹣![]() )2≥0,
)2≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有當a=b時,a+b等于2
,(只有當a=b時,a+b等于2![]() ).
).
(1)(獲得結論)在a+b≥2![]() (a、b均為正實數)中,若ab為定值p,
(a、b均為正實數)中,若ab為定值p,
則a+b≥2![]() ,只有當a=b時,a+b有最小值2
,只有當a=b時,a+b有最小值2![]() .
.
根據上述內容,回答下列問題:若m>0,只有當m= 時,m+![]() 有最小值 .
有最小值 .
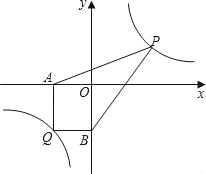
(2)(探索應用)已知點Q(﹣3,﹣4)是雙曲線y=![]() 上一點,過Q作QA⊥x軸于點A,作QB⊥y軸于點B.點P為雙曲線y=
上一點,過Q作QA⊥x軸于點A,作QB⊥y軸于點B.點P為雙曲線y=![]() (x>0)上任意一點,連接PA,PB,求四邊形AQBP的面積的最小值.
(x>0)上任意一點,連接PA,PB,求四邊形AQBP的面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知雅美服裝廠現有A種布料70米,B種布料52米,現計劃用這兩種布料生產M、N兩種型號的時裝共80套.已知做一套M型號的時裝需用A種布料1.1米,B種布料0.4米,可獲利50元;做一套N型號的時裝需用A種布料0.6米,B種布料0.9米,可獲利45元.設生產M型號的時裝套數為x,用這批布料生產兩種型號的時裝所獲得的總利潤為y元.
(1)求y(元)與x(套)的函數關系式,并求出自變量的取值范圍;
(2)當M型號的時裝為多少套時,能使該廠所獲利潤最大?最大利潤是多?
查看答案和解析>>
科目:初中數學 來源: 題型:
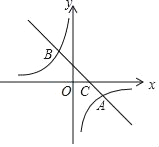
【題目】如圖,在平面直角坐標系中,一次函數y=k1x+b的圖象與反比例函數y=![]() 的圖象交于A(4,﹣2)、B(﹣2,n)兩點,與x軸交于點C.
的圖象交于A(4,﹣2)、B(﹣2,n)兩點,與x軸交于點C.
(1)求k2,n的值;
(2)請直接寫出不等式k1x+b<![]() 的解集;
的解集;
(3)將x軸下方的圖象沿x軸翻折,點A落在點A′處,連接A′B,A′C,求△A′BC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義一種新運算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代數式2x+4y+1的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com