
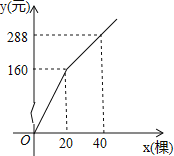
【題目】為更新樹木品種,某植物園計劃購進甲、乙兩個品種的樹苗栽植培育若計劃購進這兩種樹苗共41棵,其中甲種樹苗的單價為6元/棵,購買乙種樹苗所需費用y(元)與購買數量x(棵)之間的函數關系如圖所示.
(1)求出y與x的函數關系式;
(2)若在購買計劃中,乙種樹苗的數量不超過35棵,但不少于甲種樹苗的數量.請設計購買方案,使總費用最低,并求出最低費用.
【答案】(1)![]() ; (2) 當購買甲種樹苗20棵,乙種樹苗21棵時,使總費用最低,最低費用是286.4元
; (2) 當購買甲種樹苗20棵,乙種樹苗21棵時,使總費用最低,最低費用是286.4元
【解析】
(1)分兩種情況:①當0<x≤20時,②當x>20時,根據題意列出y與x的函數關系式即可;
(2)列式求出總費用,再根據一次函數的性質,求出總費用的最小值即可.
解:(1)設當0<x≤20時,y與x的函數關系式為y=kx,
20k=160,得k=8,
即當0<x≤20時,y與x的函數關系式為y=8x,
設當x>20時,y與x的函數關系式是y=ax+b,
![]() ,
,
得![]() ,
,
即當x>20時,y與x的函數關系式是y=6.4x+32,
由上可得y與x的函數關系式為:y=![]() ;
;
(2)∵購買乙種樹苗x棵,
∴購買甲種樹苗(41﹣x)棵,
∵在購買計劃中,乙種樹苗的數量不超過35棵,但不少于甲種樹苗的數量,
∴41﹣x≤x≤35,
解得,20.5≤x≤35,
設購買樹苗的總費用為w元,
∵20.5≤x≤35且x為整數,
∴w=(6.4x+32)+6![]() (41﹣x)=0.4x+278,
(41﹣x)=0.4x+278,
∴當x=21時,w取得最小值,此時w=286.4,41﹣x=20,
答:當購買甲種樹苗20棵,乙種樹苗21棵時,使總費用最低,最低費用是286.4元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
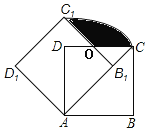
【題目】如圖,邊長為1的正方形ABCD繞點A逆時針旋轉45°后得到正方形AB1C1D1,邊B1C1與CD交于點O,則圖中陰影部分的面積是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
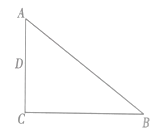
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 邊的中點.
邊的中點.
(1)尺規作圖:作出以![]() 為直徑的圓
為直徑的圓![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() .(保留作圖痕跡,不寫作法)
.(保留作圖痕跡,不寫作法)
(2)求證:![]() 是圓
是圓![]() 的切線.
的切線.
(3)當![]() 時,四邊形
時,四邊形![]() 是平行四邊形,此時,四邊形
是平行四邊形,此時,四邊形![]() 的形狀為 .
的形狀為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小紅為了更直觀了解“物體質量”的概念,各選五個雞蛋稱重,以每個![]() 為標準,大于或等于
為標準,大于或等于![]() 即為達標,超過標準部分的克數記為正數,不足標準部分的克數記為負數.小明所統計的數據為實際稱重讀數,小紅為記錄數據,把所得數據整理成如下統計表(單位:
即為達標,超過標準部分的克數記為正數,不足標準部分的克數記為負數.小明所統計的數據為實際稱重讀數,小紅為記錄數據,把所得數據整理成如下統計表(單位:![]() ).
).
序號 數據 姓名 | 1 | 2 | 3 | 4 | 5 |
小明 | 48 | 50 |
| 49 | 51 |
小紅 |
|
|
| 2 | 1 |
經過統計發現,小明所選雞蛋質量的平均數為![]() ,小紅所選雞蛋質量的眾數為
,小紅所選雞蛋質量的眾數為![]() ,根據以上信息:
,根據以上信息:
(1)填空:![]() ,
,![]() ;
;
(2)通過計算說明,小明和小紅哪個選取的雞蛋大小更均勻,請說明理由;
(3)現從小明和小紅所選取的雞蛋里各隨機挑一個,這兩個雞蛋質量都達標的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
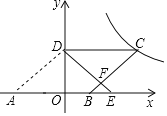
【題目】如圖,在平面直角坐標系中,O為坐標原點,ABCD的邊AB在x軸上,頂點D在y軸的正半軸上,點C在第一象限.將△AOD沿y軸翻折,使點A落在x軸上的點E處,點B恰好為OE的中點,DE與BC交于點F.若y=![]() (k≠0)圖象經過點C,且S△BEF=
(k≠0)圖象經過點C,且S△BEF=![]() ,則k的值為_____.
,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
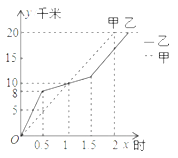
【題目】在20km越野賽中,甲乙兩選手的行程y(單位:km)隨時間x(單位:h)變化的圖象如圖所示,根據圖象信息,下列說法:①兩人相遇前,甲速度一直小于乙速度;②出發后1小時,兩人行程均為10km;③出發后1.5小時,甲的行程比乙多3km;④甲比乙先到達終點.其中正確的說法是_________(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
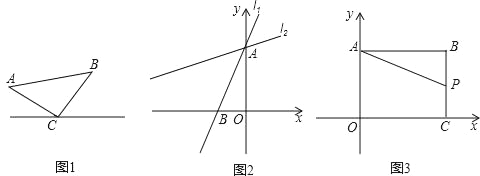
【題目】建立模型:如圖1,已知△ABC,AC=BC,∠C=90°,頂點C在直線l上.
實踐操作:過點A作AD⊥l于點D,過點B作BE⊥l于點E,求證:△CAD≌△BCE.
模型應用:(1)如圖2,在直角坐標系中,直線l1:y=![]() x+4與y軸交于點A,與x軸交于點B,將直線l1繞著點A順時針旋轉45°得到l2.求l2的函數表達式.
x+4與y軸交于點A,與x軸交于點B,將直線l1繞著點A順時針旋轉45°得到l2.求l2的函數表達式.
(2)如圖3,在直角坐標系中,點B(8,6),作BA⊥y軸于點A,作BC⊥x軸于點C,P是線段BC上的一個動點,點Q(a,2a﹣6)位于第一象限內.問點A、P、Q能否構成以點Q為直角頂點的等腰直角三角形,若能,請求出此時a的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
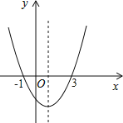
【題目】如圖,二次函數y=ax2+bx+c的圖象經過(﹣1,0)(3,0)兩點,給出的下列6個結論:
①ab<0;
②方程ax2+bx+c=0的根為x1=﹣1,x2=3;
③4a+2b+c<0;
④當x>1時,y隨x值的增大而增大;
⑤當y>0時,﹣1<x<3;
⑥3a+2c<0.
其中不正確的有_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是_____.①在同一平面內,a,b,c為直線,若a⊥b,b⊥c,則a∥c.②“若ac>bc,則a>b”的逆命題是真命題.③若M(a,2),N(1,b)關于x軸對稱,則a+b=﹣1.④一個多邊形的邊數增加1條時,內角和增加180°,外角和不變.⑤![]() 的整數部分是a,小數部分是b,則ab=3
的整數部分是a,小數部分是b,則ab=3![]() ﹣3.
﹣3.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com