
【題目】如圖,小王在長江邊某瞭望臺D處,測得江面上的漁船A的俯角為40°.若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡長BC=10米,則此時AB的長約為(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)( )

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知直線AB:y= ![]() x+4交x軸于點A,交y軸于點B.直線CD:y=﹣
x+4交x軸于點A,交y軸于點B.直線CD:y=﹣ ![]() x﹣1與直線AB相交于點M,交x軸于點C,交y軸于點D.
x﹣1與直線AB相交于點M,交x軸于點C,交y軸于點D.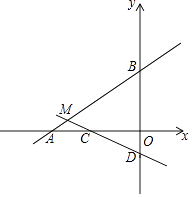
(1)直接寫出點B和點D的坐標;
(2)若點P是射線MD上的一個動點,設點P的橫坐標是x,△PBM的面積是S,求S與x之間的函數關系;
(3)當S=20時,平面直角坐標系內是否存在點E,使以點B、E、P、M為頂點的四邊形是平行四邊形?若存在,請直接寫出所有符合條件的點E的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,邊長為4,點G在邊BC上運動,DE⊥AG于E,BF∥DE交AG于點F,在運動過程中存在BF+EF的最小值,則這個最小值是 . 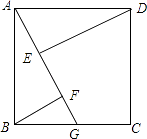
查看答案和解析>>
科目:初中數學 來源: 題型:
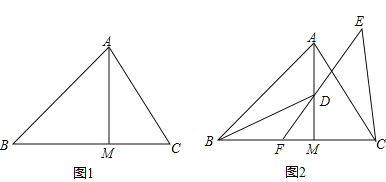
【題目】在△ABC中,∠ABM=45°,AM⊥BM,垂足為M,點C是BM延長線上一點,連接AC.
(1)如圖1,若AB=3![]() ,BC=5,求AC的長;
,BC=5,求AC的長;
(2)如圖2,點D是線段AM上一點,MD=MC,點E是△ABC外一點,EC=AC,連接ED并延長交BC于點F,且點F是線段BC的中點,求證:∠BDF=∠CEF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:探究函數y=|x|﹣2的圖象與性質.
小華根據學習函數的經驗,對函數y=|x|﹣2的圖象與性質進行了探究.
下面是小華的探究過程,請補充完整:
(1)在函數y=|x|﹣2中,自變量x可以是任意實數;
如表是y與x的幾組對應值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)為該函數圖象上不同的兩點,則n=;
(2)①如圖,在平面直角坐標系xOy中,描出以上表中各對對應值為坐標的點.并根據描出的點,畫出該函數的圖象;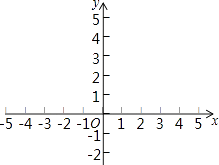
(3)該函數的最小值為;
(4)已知直線 ![]() 與函數y=|x|﹣2的圖象交于C、D兩點,當y1≥y時x的取值范圍是 .
與函數y=|x|﹣2的圖象交于C、D兩點,當y1≥y時x的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列一段文字,然后回答下列問題.
已知在平面內兩點P1(x1 , y1)、P2(x2 , y2),其兩點間的距離 ![]() ,
,
同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可簡化為|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),試求A、B兩點間的距離;
(2)已知A、B在平行于y軸的直線上,點A的縱坐標為4,點B的縱坐標為﹣1,試求A、B兩點間的距離;
(3)已知一個三角形各頂點坐標為D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形狀嗎?說明理由;
(4)平面直角坐標中,在x軸上找一點P,使PD+PF的長度最短,求出點P的坐標以及PD+PF的最短長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com