
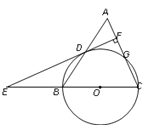
【題目】如圖,等腰三角形ABC中,AC=BC=10,AB=12. 以BC為直徑作⊙O交AB于點D,交AC于點G,DF⊥AC,垂足為F,交CB的延長線于點E.
(1)求證:直線EF是⊙O的切線;
(2)求sin∠E的值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)求證直線EF是⊙O的切線,只要連接OD證明OD⊥EF即可;
(2)根據∠E=∠CBG,可以把求sin∠E的值得問題轉化為求sin∠CBG,進而轉化為求Rt△BCG中,兩邊的比的問題.
(1)連結OD, CD.
∵BC是直徑,
∴CD⊥AB.
∵AC=BC,
∴D是AB的中點.
又O為BC中點,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
∴直線EF是⊙O的切線.
(2)連結BG.
∵BC是直徑,
∴∠BGC=90°.
在Rt△BCD中, CD=![]() .
.
∵![]() AB·CD=
AB·CD=![]() AC·BG,
AC·BG,
∴BG=![]() .
.
在Rt△BGC中, CG=![]() .
.
∵BG∥EF,
∴∠E=∠CBG.
∴sin∠E=sin∠CBG=![]() .
.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線AB與函數y=![]() (x>0)的圖象交于點A(m,2),B(2,n).過點A作AC平行于x軸交y軸于點C,在y軸負半軸上取一點D,使OD=
(x>0)的圖象交于點A(m,2),B(2,n).過點A作AC平行于x軸交y軸于點C,在y軸負半軸上取一點D,使OD=![]() OC,且△ACD的面積是6,連接BC.
OC,且△ACD的面積是6,連接BC.
(1)求m,k,n的值;
(2)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10,點D是邊BC上一動點 (不與B,C重合),∠ADE=∠B=α,DE交AC于點E,且 ![]() .下列結論: ①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8或
.下列結論: ①△ADE∽△ACD;②當BD=6時,△ABD與△DCE全等;③△DCE為直角三角形時,BD為8或![]() ;④CD2=CECA.其中正確的結論是________(把你認為正確結論的序號都填上)
;④CD2=CECA.其中正確的結論是________(把你認為正確結論的序號都填上)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB為⊙O的直徑,PC切⊙O于C交AB的延長線于點P,∠CAP=35°,那么∠CPO的度數等于( )
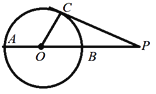
A. 15° B. 20° C. 25° D. 30°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠MAN=30°,O為邊AN上一點,以點O為圓心,2為半徑作⊙O,交AN于D,E兩點,設AD=x.
(1)如圖①,當x取何值時,⊙O與AM相切?
(2)如圖②,當x為何值時,⊙O與AM相交于B,C兩點,且∠BOC=90°?
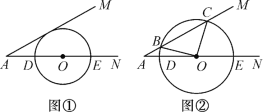
查看答案和解析>>
科目:初中數學 來源: 題型:
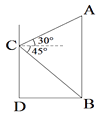
【題目】某數學興趣小組的同學在一次活動中,為了測量某建筑物AB的高,他們來到另一建筑物CD上的點C處進行觀察,如圖所示,他們測得建筑物AB頂部A的仰角為30°,底部B的俯角為45°,已知建筑物AB、CD的距離DB為12m,求建筑物AB的高.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是從一副撲克牌中取出的兩組牌,分別是黑桃1,2,3,4和方塊1,2,3,4,將它們背面朝上分別重新洗牌后,從兩組牌中各摸出一張,那么摸出的兩張牌的牌面數字之和等于5的概率是多少?請你用列舉法(列表或畫樹狀圖)加以分析說明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鳳城商場經銷一種高檔水果,售價為每千克50元
(1)連續兩次降價后售價為每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知這種水果的進價為每千克40元,每天可售出500千克,經市場調查發現,若每千克漲價1元,日銷售量將減少20千克,每千克應漲價多少元才能使每天獲得的利潤最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() 與x、y軸分別交于點A、C.拋物線的圖象經過A、C和點B(1,0).
與x、y軸分別交于點A、C.拋物線的圖象經過A、C和點B(1,0).

(1)求拋物線的解析式;
(2)在直線AC上方的拋物線上有一動點D,當D與直線AC的距離DE最大時,求出點D的坐標,并求出最大距離是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com