
【題目】(1)小My同學在網絡直播課中學習了勾股定理,他想把這一知識應用在等邊三角形中:邊長為a的等邊三角形面積是 (用含a的代數式表示);
(2)小My同學進一步思考:是否可以將正方形剪拼成一個等邊三角形(不重疊、無縫隙)?
①如果將一個邊長為2的正方形紙片剪拼等邊三角形,那么該三角形邊長的平方是 ;
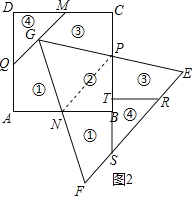
②小My同學按下圖切割方法將正方形ABCD剪拼成一個等邊三角形EFG:M、N分別為AB、CD邊上的中點,P、Q是邊BC、AD上兩點,G為MQ上一點,且∠MGP=∠PGN=∠NGQ=60°.
請補全圖形,畫出拼成正三角形的各部分分割線,并標號;
③正方形ABCD的邊長為2,設BP=x,則x2= .

【答案】(1)![]() a2;(2)①
a2;(2)①![]() ;②詳見解析;③
;②詳見解析;③![]() ﹣1.
﹣1.
【解析】
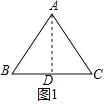
(1)如圖1,過A作AD⊥BC于D,根據等邊三角形的性質得到BD=CD=![]() BC=
BC=![]() a,由勾股定理得到AD=
a,由勾股定理得到AD=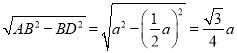 ,于是得到S△ABC=
,于是得到S△ABC=![]() BCAD=
BCAD=![]() ;
;
(2)①根據三角形的面積公式即可得到結論;
②補全圖形如圖2所示;
③由題意知,PG=PE,GN=NF,推出PN是△GEF的中位線,得到PN=![]() EF,根據勾股定理即可得到結論.
EF,根據勾股定理即可得到結論.
解:(1)如圖,過A作AD⊥BC于D,
∵△ABC是等邊三角形,
∴BD=CD=![]() BC=
BC=![]() a,
a,
∴AD=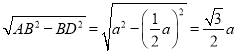 ,
,
∴S△ABC=![]() BCAD=
BCAD=![]() a2;
a2;
(2)①∵邊長為2的正方形的面積=4,
∴剪拼成的等邊三角形的面積=4,
∴![]() a2=4,
a2=4,
∴a2=![]() ,
,
即該三角形邊長的平方是![]() ;
;
②補全圖形如圖2所示;
③由題意知,PG=PE,GN=NF,
∴PN是△GEF的中位線,
∴PN=![]() EF,
EF,
∵N為AB邊上的中點,
∴BN=![]() AB=1,
AB=1,
∵邊長為2的正方形的面積=4,
∴剪拼成的等邊三角形的面積=4,
∴![]() a2=4,
a2=4,
∴a2=![]() ,
,
即△GEF邊長的平方是![]() ,
,
∴EF=![]() ,
,
∴PN=![]() ,
,
∵PN2=BN2+BP2,
∴![]() =1+x2,
=1+x2,
∴x2=![]() ﹣1;
﹣1;
故答案為:(1)![]() ;(2)①
;(2)①![]() ;③
;③![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 為線段
為線段![]() 上的一個動點,分別以
上的一個動點,分別以![]() ,
,![]() 為邊在
為邊在![]() 的同側作菱形
的同側作菱形![]() 和菱形
和菱形![]() ,點
,點![]() ,
,![]() ,
,![]() 在一條直線上,
在一條直線上,![]() ,
,![]() 、
、![]() 分別是對角線
分別是對角線![]() ,
,![]() 的中點,當點
的中點,當點![]() 在線段
在線段![]() 上移動時,線段
上移動時,線段![]() 的最小值為________.
的最小值為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知: ![]() 和矩形
和矩形![]() 如圖①擺放(點
如圖①擺放(點![]() 與點
與點![]() 重合),點
重合),點![]() ,
, ![]() 在同一直線上,
在同一直線上, ![]() ,
, ![]() ,
, ![]() .如圖②,
.如圖②,![]() 從圖①的位置出發,沿
從圖①的位置出發,沿![]() 方向勻速運動,速度為1
方向勻速運動,速度為1 ![]() ,
, ![]() 與
與![]() 交于點
交于點![]() ,與BD交于點K;同時,點
,與BD交于點K;同時,點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向勻速運動,速度為1
方向勻速運動,速度為1 ![]() .過點
.過點![]() 作
作![]() ,垂足為
,垂足為![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,當點
,當點![]() 停止運動時,
停止運動時, ![]() 也停止運動.設運動事件為
也停止運動.設運動事件為![]() .解答下列問題:
.解答下列問題:
(1)當為何值時, ![]() ?
?
(2)在運動過程中,是否存在某一時刻,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)在運動過程中,
①當t為 秒時,以PQ為直徑的圓與PE相切,
②當t為 秒時,以PQ的中點為圓心,以 cm為半徑的圓與BD和BC同時相切.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() ,點
,點![]() 是直線
是直線![]() 、
、![]() 之間的一點,連接
之間的一點,連接![]() 、
、![]() .
.
(1)探究猜想:
①若![]() ,則
,則![]() .
.
②若![]() ,則
,則![]() .
.
③猜想圖1中![]() 、
、![]() 、
、![]() 的關系,并證明你的結論.
的關系,并證明你的結論.
(2)拓展應用:
如圖2,![]() ,線段
,線段![]() 把
把![]() 這個封閉區域分為I、II兩部分(不含邊界),點
這個封閉區域分為I、II兩部分(不含邊界),點![]() 是位于這兩個區域內的任意一點,請直接寫出
是位于這兩個區域內的任意一點,請直接寫出![]() 、
、![]() 、
、![]() 的關系.
的關系.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】函數y=x2+bx+c與y=x的圖象如圖所示,有以下結論:
①b2﹣4c>0;②b+c=0;③2b+c+3=0;④當1<x<3時,x2+(b﹣1)x+c<0
其中正確的有( )個.

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖A在數軸上對應的數為-2.
(1)點B在點A右邊距離A點4個單位長度,則點B所對應的數是_____.
(2)在(1)的條件下,點A以每秒2個單位長度沿數軸向左運動,點B以每秒3個單位長度沿數軸向右運動.現兩點同時運動,當點A運動到-6的點處時,求A、B兩點間的距離.
(3)在(2)的條件下,現A點靜止不動,B點以原速沿數軸向左運動,經過多長時間A、B兩點相距4個單位長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
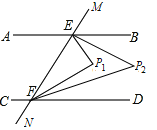
【題目】如圖,已知直線AB∥CD,MN分別交AB,CD于點E,F,∠BEF與∠DFE的兩條平分線相交于點P1,∠BEP1與∠DFP1的兩條平分線相交于點P2,則∠P2的度數為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一個由小正方體組成的幾何體的左視圖和俯視圖.

![]() 該幾何體最少需要幾塊小正方體?最多可以有幾塊小正方體?
該幾何體最少需要幾塊小正方體?最多可以有幾塊小正方體?
![]() 請畫出該幾何體的所有可能的主視圖.
請畫出該幾何體的所有可能的主視圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為預防疾病,某校對教室進行“藥熏消毒”.已知藥物燃燒階段,室內每立方米空氣中的含藥量![]() (mg)與燃燒時間
(mg)與燃燒時間![]() (分鐘)成正比例;燃燒后,
(分鐘)成正比例;燃燒后, ![]() 與
與![]() 成反比例(如圖所示).現測得藥物10分鐘燃完,此時教室內每立方米空氣含藥量為8mg.據以上信息解答下列問題:
成反比例(如圖所示).現測得藥物10分鐘燃完,此時教室內每立方米空氣含藥量為8mg.據以上信息解答下列問題:
(1)求藥物燃燒時![]() 與
與![]() 的函數關系式.(2)求藥物燃燒后
的函數關系式.(2)求藥物燃燒后![]() 與
與![]() 的函數關系式.
的函數關系式.
(3)當每立方米空氣中含藥量低于1.6mg時,對人體方能無毒害作用,那么從消毒開始,經多長時間學生才可以回教室?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com