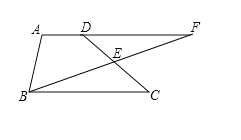
【題目】已知：如圖，梯形ABCD中，AD∥BC，點E是CD的中點，BE的延長線與AD的延長線相交于點F．
（1）求證：△BCE≌△FDE．
（2）連接BD，CF，判斷四邊形BCFD的形狀，并證明你的結論．
【答案】（1）見解析；（2）四邊形BCFD是平行四邊形，理由見解析
【解析】
（1）由平行線的性質可證，∠DFE=∠EBC，∠FDE=∠ECB，又已知DE=CE，在△BCE與△FDE中，根據三角形全等的判定定理，符合AAS的條件，即證△BCE≌△FDE．
（2）在1的基礎上，可證DE=CE，FE=BE，根據平行四邊形的判定，即證四邊形BCFD是平行四邊形．
證明：（1）∵點E是DC中點∴DE=CE
又∵AD∥BC，F在AD延長線上，∴∠DFE=∠EBC，∠FDE=∠ECB
在△BCE與△FDE中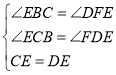
．
∴△BCE≌△FDE（AAS）
（2）四邊形BCFD是平行四邊形．理由如下：
∵△BCE≌△FDE，
∴DE=CE，FE=BE．
∴四邊形BCFD是平行四邊形．．
科目：初中數學 來源： 題型：
【題目】為提高中小學生的身體素質，各校大力開展校園足球活動，某體育用品商店抓住這一商機，第一次用30000元購進A、B兩種型號的足球，并很快銷售完，共獲利12200元，其進價和售價如下表：
A | B | |
進價/（元/個） | 120 | 200 |
售價/（元/個） | 170 | 280 |
（1）體育用品商店購進A、B兩種型號的足球各多少個？
（2）該體育用品商店第二次準備用不超過40000元的資金再次購進A、B兩種型號的足球共260個，最少購進A種型號的足球多少個？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖（1），在Rt△ABC中，∠A=90°，AC=AB=4，D，E分別是AB，AC的中點．若等腰Rt△ADE繞點A逆時針旋轉，得到等腰Rt△AD1E1，如圖（2），設旋轉角為α（0＜α≤180°），記直線BD1與CE1的交點為P．
（1）求證：BD1=CE1；（2）當∠CPD1=2∠CAD1時，求CE1的長；
（3）連接PA，△PAB面積的最大值為 ．（直接填寫結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在某種特制的計算器中有一個按鍵
，它代表運算
．
例如：
上述操作即是求
的值，運算結果為1．
回答下面的問題：
（1）小敏的輸入順序為﹣6，
，﹣8，
，運算結果是 ；
（2）小杰的輸入順序為1，，-
，，，﹣2，
，-
，，
，3，，運算結果是 ；
（3）若在
這些數中，任意選取兩個作為a、b的值，進行
運算，則所有的運算結果中最大的值是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
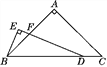
【題目】如圖，△ABC中，AB＝AC，∠BAC＝90°，點D在線段BC上，∠EDB＝
∠C，BE⊥DE，垂足為E，DE與AB相交于點F.試探究線段BE與DF的數量關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，我們把對角線互相垂直的四邊形叫做垂美四邊形．
(l)概念理解：如圖2，在四邊形ABCD中，AB=AD，CB=CD，問四邊形ABCD是垂美四邊形嗎？請說明理由．
(2)性質探宄：試探索垂美四邊形ABCD兩組對邊AB，CD與BC，AD之間的數量關系．
猜想結論:（要求用文字語言敘述）
寫出證明過程（先畫出圖形，寫出已知、求證）
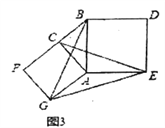
(3)問題解決：如圖3，分別以Rt△ACB的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE，連接CE，BG，GE，已知AC=4，AB=5,求GE長．
查看答案和解析>>
科目：初中數學 來源： 題型：
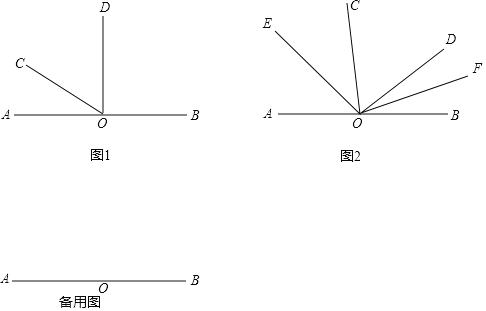
【題目】已知：如圖1，點O是直線AB上的一點．
（1）如圖1，當∠AOD是直角時，3∠AOC＝∠BOD，求∠COD的度數；
（2）若∠COD保持在（1）中的大小不變，它繞著點O順時針旋轉（OD與OB重合即停止），如圖2，OE、OF分別平分∠AOC、∠BOD，則在旋轉過程中∠EOF的大小是否變化？若不變，求出∠EOF的大小；若改變，說明理由；
（3）若∠COD從（1）中的位置開始，邊OC、邊OD分別繞著點O以每秒20°、每秒10°的速度順時針旋轉（當其中一邊與OB重合時都停止旋轉），OM、ON分別平分∠BOC、∠BOD．
求：①運動多少秒后，∠COD＝10°；
②運動多少秒后，∠COM＝∠BON．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
