
【題目】先化簡,再求值:5(3a2b-ab2)-4(-ab2+3a2b), 其中a=-1,b=-2.
 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(﹣1,1),B(﹣4,2),C(﹣3,4).
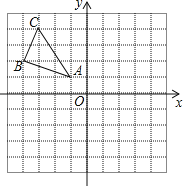
(1)請畫出△ABC向右平移5個單位長度后得到△A1B1C1;
(2)請畫出△ABC關于原點對稱的△A2B2C2;
(3)在x軸上求作一點P,使△PAB的周長最小,并直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小華進行了5次射擊訓練后,計算出這5次射擊的平均成績為8環,方差為s12 , 隨后小華又進行了第6次射擊,成績恰好是8環,并計算出這6次射擊成績的方差為s22 , 則下列說法正確的是( )
A.s12=s22
B.s12<s22
C.s12>s22
D.無法確定s12與s22的大小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究與發現:
探究一:我們知道,三角形的一個外角等于與它不相鄰的兩個內角的和.那么,三角形的一個內角與它不相鄰的兩個外角的和之間存在何種數量關系呢?
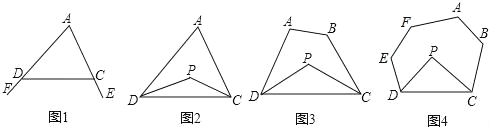
已知:如圖1,∠FDC與∠ECD分別為△ADC的兩個外角,試探究∠A與∠FDC+∠ECD的數量關系.
探究二:三角形的一個內角與另兩個內角的平分線所夾的鈍角之間有何種關系?
已知:如圖2,在△ADC中,DP、CP分別平分∠ADC和∠ACD,試探究∠P與∠A的數量關系.
探究三:若將△ADC改為任意四邊形ABCD呢?
已知:如圖3,在四邊形ABCD中,DP、CP分別平分∠ADC和∠BCD,試利用上述結論探究∠P與∠A+∠B的數量關系.
探究四:若將上題中的四邊形ABCD改為六邊形ABCDEF(圖4)呢?
請直接寫出∠P與∠A+∠B+∠E+∠F的數量關系: .
查看答案和解析>>
科目:初中數學 來源: 題型:
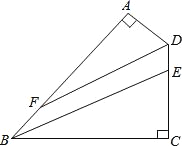
【題目】如圖,四邊形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.
(1)若∠ABC=50°,則∠ADC= °,∠AFD= °;
(2)BE與DF平行嗎?試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com