
我們解一元二次方程3x2﹣6x=0時,可以運用因式分解法,將此方程化為3x(x﹣2)=0,從而得到兩個一元一次方程:3x=0或x﹣2=0,進而得到原方程的解為x1=0,x2=2.這種解法體現的數學思想是( )
|
| A. | 轉化思想 | B. | 函數思想 | C. | 數形結合思想 | D. | 公理化思想 |
 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
在“愛滿揚州”慈善一日捐活動中,學校團總支為了了解本校學生的
捐款情況,隨機抽取了50名學生的捐款數進行了統計,并繪制成下面的統計圖。
(1)這50名同學捐款的眾數為 元,中位數為 元
 (2)求這50名同學捐款的平均數
(2)求這50名同學捐款的平均數
(3)該校共有600名學生參與捐款,請估計該校學生 的捐款總數
的捐款總數

查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,直線⊥線段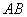 于點
于點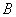 ,點
,點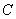 在
在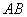 上,且
上,且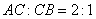 ,點
,點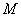 是直線上的動點,作點
是直線上的動點,作點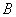 關于直線
關于直線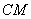 的對稱點
的對稱點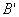 ,直線
,直線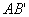 與直線
與直線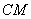 相交于點
相交于點 ,連接
,連接
(1)如圖1,若點 與點
與點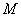 重合,則∠
重合,則∠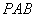 = °,線段
= °,線段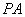 與
與 的比值為 ;
的比值為 ;
(2)如圖2,若點 與點
與點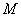 不重合,設過
不重合,設過 、
、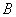 、
、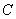 三點的圓與直線
三點的圓與直線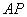 相交于
相交于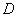 ,
,
連接 。
。
求證:① =
=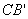 ;②
;②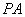 =2
=2 ;
;
(3)如圖3,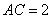 ,
, ,則滿足條件
,則滿足條件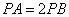 的點都在一個確定的圓上,在
的點都在一個確定的圓上,在
以下兩小題中選做一題:
①如果你能發現這個確定圓的圓心和半徑,那么不必寫出發現過程,只要證明這個
圓上的任意一點Q,都滿足QA=2QB
②如果你不能發現這個確定圓的圓心和半徑,那么請取幾個特殊位置的 點,如點
點,如點 在直線
在直線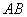 上、點
上、點 與點
與點 重合等進行探究,求這個圓的半徑
重合等進行探究,求這個圓的半徑

查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,把Rt△ABC放在直角坐標系內,其中∠CAB=90°,BC=5,點A、B的坐標分別為(1,0)、(4,0).將△ABC沿x軸向右平移,當點C落在直線y=2x﹣6上時,線段BC掃過的面積為( )
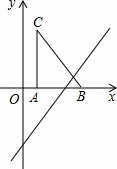
|
| A.] | 4 | B. | 8 | C. | 16 | D. | 8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com