【題目】如圖，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分線，DE⊥AB，垂足為E．
（1）已知CD=4cm，求AC的長；
（2）求證：AB=AC+CD．
【答案】（1）
；（2）證明見試題解析．
【解析】
試題分析：（1）由角平分線的性質可知CD=DE=4cm，由于∠C=90°，故∠B=∠BDE=45°，△BDE是等腰直角三角形，由勾股定理得可得BD，AC的值；
（2）由（1）可知：△ACD≌△AED，AC=AE，BE=DE=CD，故AB=AE+BE=AC+CD．
試題解析：（1）∵AD是△ABC的角平分線，DC⊥AC，DE⊥AB，∴DE=CD=4cm，又∵AC=BC，∴∠B=∠BAC，又∵∠C=90°，∴∠B=∠BDE=45°，∴BE=DE=4cm．
在等腰直角三角形BDE中，由勾股定理得，BD=
cm，∴AC=BC=CD+BD=（cm）．
（2）∵AD是△ABC的角平分線，DC⊥AC，DE⊥AB，∴∠ADE=∠ADC，∴AC=AE，又∵BE=DE=CD，∴AB=AE+BE=AC+CD．
新課標同步訓練系列答案科目：初中數學 來源： 題型：
【題目】閱讀材料：
若a，b都是非負實數，則a＋b≥2
.當且僅當a＝b時，“＝”成立．
證明： ∵(
－
)2≥0，∴a－2
＋b≥0.
∴a＋b≥2
.當且僅當a＝b時，“＝”成立．
舉例應用：
已知x>0，求函數y＝2x＋
的最小值．
解：y＝2x＋
≥2
＝4.當且僅當2x＝
，即x＝1時，“＝”成立．
當x＝1時，函數取得最小值，y最小＝4.
問題解決：
汽車的經濟時速是指汽車最省油的行駛速度．某種汽車在每小時70～110公里之間行駛(含70公里和110公里)，每公里耗油(
＋
)升．若該汽車以每小時x公里的速度勻速行駛，1小時的耗油量為y升．
(1)求y關于x的函數關系式(寫出自變量x的取值范圍)；
(2)求該汽車的經濟時速及經濟時速的百公里耗油量(結果保留小數點后一位)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把二次函數y=a(x-h)2+k的圖象先向左平移2個單位，再向上平移4個單位，得到二次函數y=
(x+1)2-1的圖象.
（1）試確定a，h，k的值；
（2）指出二次函數y=a(x-h)2+k的開口方向，對稱軸和頂點坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
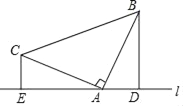
【題目】已知：如圖所示，△ABC中，∠BAC=90°，AB=AC，分別過點B、C作經過點A的直線l的垂線段BD、CE，垂足分別D、E．
（1）求證：DE=BD+CE．
（2）如果過點A的直線經過∠BAC的內部，那么上述結論還成立嗎？請畫出圖形，直接給出你的結論（不用證明）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
