
如圖,已知直線y=-2x+4與x軸、y軸分別相交于A、C兩點,拋物線
y=-2x +bx+c (a≠0)經過點A、C.
+bx+c (a≠0)經過點A、C.

1.求拋物線的解析式;
2.設拋物線的頂點為P,在拋物線上存在點Q,使△ABQ的面積等于△APC面積的4倍.求出點Q的坐標;
3.點M是直線y=-2x+4上的動點,過點M作ME垂直x軸于點E,在y軸(原點除外)上是否存在點F,使△MEF為等腰直角三角形? 若存在,求出點F的坐標及對應的點M的坐標;若不存在,請說明理由
1.在 中,當
中,當 時,
時,
當 時,
時,
∴A(2,0) ,
C(0,4) 代入
則 1分
1分
有 2分
2分
∴拋物線解析式為 3分
3分
2.當 時,
時,  ∴
∴
過P作PD⊥ 軸于D
軸于D
 , OC=4,OD=
, OC=4,OD=
∴CD= ,
DP=
,
DP= ∴
∴



∴
 4分
4分
設△ABQ中AB邊上的高為 ,
, 
當 時,
時,

 ,
, 
∴ ∴
∴
由題意
∴
 5分
5分
設 或
或
當


當 ,
,  ,
,
∴Q1(0,4) , Q2(1,4),
 ,
,  7分
7分
3.若存在點F使△MEF為等腰直角三角形,設
∵F不在原點, ∴點E不為直角頂點
①當M為直角頂點時,有
若 同號(同正,即M在一象限)
同號(同正,即M在一象限)
則 ,即
,即

 ∴
∴ ,此時
,此時
若 異號(M在二或四象限), 則
異號(M在二或四象限), 則 , 即
, 即 ,
, 
∴M2(4,-4) 此時 9分
9分
②當F為直角頂點時,有
若 同號(M在一象限) 則
同號(M在一象限) 則
即 ,
,  ,
,  ,
∴
,
∴ , 此時F3(0,1)
, 此時F3(0,1)
若 異號(M在二象限或四象限)
異號(M在二象限或四象限)
則 , 即
, 即 , 此方程無解.
, 此方程無解.
∴存在△MEF為等腰直角三角形,其坐標為
 ;
;  ;
; 
【解析】略


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
如圖,已知直線y=-2x+4與x軸、y軸分別相交于A、C兩點,拋物線
y=-2x![]() +bx+c (a≠0)經過點A、C.
+bx+c (a≠0)經過點A、C.

1.求拋物線的解析式;
2.設拋物線的頂點為P,在拋物線上存在點Q,使△ABQ的面積等于△APC面積的4倍.求出點Q的坐標;
3.點M是直線y=-2x+4上的動點,過點M作ME垂直x軸于點E,在y軸(原點除外)上是否存在點F,使△MEF為等腰直角三角形? 若存在,求出點F的坐標及對應的點M的坐標;若不存在,請說明理由
查看答案和解析>>
科目:初中數學 來源:2010-2011學年江蘇省姜堰市初二下學期期中考試數學卷 題型:解答題
如圖:已知直線y=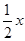 與雙曲線y=
與雙曲線y= 交于A、B兩點,且點A的橫坐標為4
交于A、B兩點,且點A的橫坐標為4
⑴求k的值;
⑵若雙曲線y= 上的一點C的縱坐標為8,求△AOC的面積?
上的一點C的縱坐標為8,求△AOC的面積?
查看答案和解析>>
科目:初中數學 來源:2013-2014學年福建莆田青璜中學九年級下學期期初考試數學試卷(解析版) 題型:解答題
如圖,已知直線y=-2x+4與x軸、y軸分別相交于A、C兩點,拋物線y=-2x2+bx+c (a≠0)經過點A、C.

(1)求拋物線的解析式;
(2)設拋物線的頂點為P,在拋物線上存在點Q,使△ABQ的面積等于△APC面積的4倍.求出點Q的坐標;
(3)點M是直線y=-2x+4上的動點,過點M作ME垂直x軸于點E,在y軸(原點除外)上是否存在點F,使△MEF為等腰直角三角形? 若存在,求出點F的坐標及對應的點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2012屆重慶市初二下學期期中考試數學卷 題型:解答題
如圖:已知直線y= 與雙曲線y=
與雙曲線y= 交于A、B兩點,且點A的橫坐標為4
交于A、B兩點,且點A的橫坐標為4

⑴求k的值;
⑵若雙曲線y= 上的一點C的縱坐標為8,求△AOC的面積?
上的一點C的縱坐標為8,求△AOC的面積?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com