
【題目】如圖,在平面直角坐標系內,點![]() 為坐標原點,
為坐標原點,![]() 的頂點
的頂點![]() 在
在![]() 軸正半軸,頂點
軸正半軸,頂點![]() 、
、![]() 分別在
分別在![]() 軸負半軸和正半軸上,
軸負半軸和正半軸上,![]() ,
,![]() ,
,![]()
(1)求![]() 的長.
的長.
(2)動點![]() 從點
從點![]() 出發以每秒
出發以每秒![]() 個單位長度的速度沿
個單位長度的速度沿![]() 向終點
向終點![]() 運動,點
運動,點![]() 運動的時間為
運動的時間為![]() ,以
,以![]() 為斜邊在
為斜邊在![]() 右邊上方作等腰直角三角形
右邊上方作等腰直角三角形![]() ,連接
,連接![]() 、
、![]() ,設
,設![]() 的面積為
的面積為![]() (
(![]() ),求
),求![]() 與
與![]() 之間的函數關系式,并直接寫出自變量
之間的函數關系式,并直接寫出自變量![]() 的取值范圍.
的取值范圍.
(3)在(2)的條件下,過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于
軸于![]() ,連接
,連接![]() ,當四邊形
,當四邊形![]() 的面積為
的面積為![]() ,時,求
,時,求![]() 的值及
的值及![]() 點坐標.
點坐標.
【答案】(1)![]() ;(2)S=2t(0≤t≤4);(3)Q(0,-2).
;(2)S=2t(0≤t≤4);(3)Q(0,-2).
【解析】
(1)根據三角形面積公式求得BC的長,然后根據等腰三角形的性質求OB的長,從而利用勾股定理求解;
(2)作PM⊥BC于N,DH⊥PC于H.利用勾股定理求出PC的長(用t表示)即可解決問題;
(3)作PN⊥y軸于N,DK⊥PN于K,DH⊥PC于H,連接AH、DH.首先證明A、P、D、C四點共圓,推出∠DAC=∠DPC=45°,∠DAO=90°,由△PNQ≌△DKP,可得DP=PQ=DC,可得四邊形PQCD是正方形,根據題意列出方程即可解決問題;
解:∵![]()
∴BC=8
又∵![]() 的頂點
的頂點![]() 在
在![]() 軸正半軸,頂點
軸正半軸,頂點![]() 、
、![]() 分別在
分別在![]() 軸負半軸和正半軸上,
軸負半軸和正半軸上,![]() ,
,
∴OB=OC=![]() ,
,
∴在Rt△OAB中,![]()
(2)如圖1中,作DM⊥X軸于M,PK⊥DM于K交y軸于N,DH⊥PC于H,作PE⊥x軸于E,連接AH、DH.
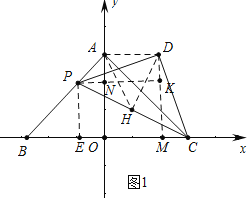
由(1)可知,OA=OB=4
∴∠BAO=∠CAO=45°,即∠BAC=90°
又∵△PCD是等腰直角三角形
∴AH=DH=HP=HC,
∴A、P、D、C四點共圓,
∴∠DAC=∠DPC=45°,
∴∠DAO=90°,
∵∠DPK+∠PDM=90°,∠PDM+∠MDC=90°,
∴∠DPK=∠MDC,
∵∠PKD=∠DMC=90°,DP=DC,
∴△PDK≌△DCM,
∴PK=DM=OA=4,
∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形,
∵PE⊥BC,
∴∠PEB=90°,
∴∠PBE=∠BPE=45°,
∵PB=![]() t,
t,
由題意可知,四邊形PEON為矩形
∴PE=BE=t,ON=4-t,
∴CM=DK=AN=OA=ON=OA-PE=4-t,
∴AD=4-(4-t)=t,
∴S=![]()
![]() t4=2t(0≤t≤4).
t4=2t(0≤t≤4).
(3)如圖2中,
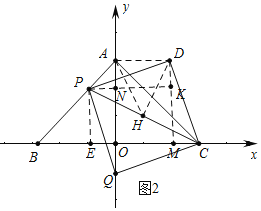
由(2)可知:PE=BE=t,ON=4-t,CE=8-t,
在Rt△PCE中,PC2=t2+(8-t)2=2t2-16t+64,
∵△PDC是等腰直角三角形,DH⊥PC,
∴PH=CH=DH,
∴S△PDC=![]() =
=![]() (0≤t≤4).
(0≤t≤4).
易知AN=PN=DK,∠QPN=∠PDK,∠PNQ=∠PKD=90°,
∴△PNQ≌△DKP,
∴DP=PQ=DC,∵PQ∥DC,
∴四邊形PQCD是平行四邊形,
∵∠DPQ=90°,
∴四邊形PQCD是矩形,
∵PD=PQ,
∴四邊形PQCD是正方形,
由題意:2(![]() )=
)=![]() ,
,
2(![]() )=10t
)=10t
整理得t2-8t+32=0,
解得:t=2或16(舍棄),
∴t=2時,四邊形PDCQ的面積為20,
此時PC=2![]() ,PQ=2
,PQ=2![]() ,PN=2,ON=2,NQ=
,PN=2,ON=2,NQ=![]() =4,
=4,
∴OQ=QN-ON=2,
∴Q(0,-2).


科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(
的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(![]() ,﹣2);⑤當x<
,﹣2);⑤當x<![]() 時,y隨x的增大而減小;⑥a+b+c>0正確的有( )
時,y隨x的增大而減小;⑥a+b+c>0正確的有( )

A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店用1000元人民幣購進水果銷售,過了一段時間,又用2400元人民幣購進這種水果,所購數量是第一次購進數量的2倍,但每千克的價格比第一次購進的貴了2元.
(1)該商店第一次購進水果多少千克;
(2)假設該商店兩次購進的水果按相同的標價銷售,最后剩下的20千克按標價的五折優惠銷售.若兩次購進水果全部售完,利潤不低于950元,則每千克水果的標價至少是多少元?
注:每千克水果的銷售利潤等于每千克水果的銷售價格與每千克水果的購進價格的差,兩批水果全部售完的利潤等于兩次購進水果的銷售利潤之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】再讀教材:寬與長的比是![]() (約為
(約為![]() )的矩形叫做黃金矩形,黃金矩形給我們以協調、勻稱的美感.世界各國許多著名的建筑,為取得最佳的視覺效果,都采用了黃金矩形的設計,下面我們用寬為
)的矩形叫做黃金矩形,黃金矩形給我們以協調、勻稱的美感.世界各國許多著名的建筑,為取得最佳的視覺效果,都采用了黃金矩形的設計,下面我們用寬為![]() 的矩形紙片折疊黃金矩形(提示:
的矩形紙片折疊黃金矩形(提示:![]() )
)
第一步:在矩形紙片一端利用圖①的方法折出一個正方形,然后把紙片展平.

第二步:如圖②,把這個正方形折成兩個相等的矩形,再把紙片展平.

第三步:折出內側矩形的對角線![]() ,并把
,并把![]() 折到圖③中所示的
折到圖③中所示的![]() 處.
處.

第四步:展平紙片,按照所得的點![]() 折出
折出![]() 使
使![]() 則圖④中就會出現黃金矩形.
則圖④中就會出現黃金矩形.

問題解決:
(1)圖③中![]() _ (保留根號);
_ (保留根號);
(2)如圖③,判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)請寫出圖④中所有的黃金矩形,并選擇其中一個說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某青春黨支部在精準扶貧活動中,給結對幫扶的貧困家庭贈送甲、乙兩種樹苗讓其栽種.已知乙種樹苗的價格比甲種樹苗貴10元,用480元購買乙種樹苗的棵數恰好與用360元購買甲種樹苗的棵數相同.
(1)求甲、乙兩種樹苗每棵的價格各是多少元?
(2)在實際幫扶中,他們決定再次購買甲、乙兩種樹苗共50棵,此時,甲種樹苗的售價比第一次購買時降低了10%,乙種樹苗的售價不變,如果再次購買兩種樹苗的總費用不超過1500元,那么他們最多可購買多少棵乙種樹苗?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學組織學生到商場參加社會實踐活動,他們參與了某種品牌運動鞋的銷售工作,已知該運動鞋每雙的進價為120元,為尋求合適的銷售價格進行了4天的試銷,試銷情況如表所示:

(1)觀察表中數據,x,y滿足什么函數關系?請求出這個函數關系式;
(2)若商場計劃每天的銷售利潤為3000元,則其單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的部分圖象如圖,圖象過點
的部分圖象如圖,圖象過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④當
;④當![]() 時,
時, ![]() 的值隨
的值隨![]() 值的增大而增大;⑤當函數值
值的增大而增大;⑤當函數值![]() 時,自變量
時,自變量![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .其中正確的結論有__________.
.其中正確的結論有__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△BDE都是等邊三角形,點A,B,D在一條直線上。給出4個結論:①AE=CD;②AB⊥FB;③∠AFC=60°;④△BGH是等邊三角形。其中正確的是( )
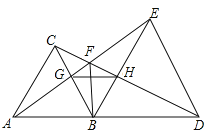
A.①,②,③B.①,②,④
C.①,③,④D.②,③,④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶市有![]() 五個景區很受游客喜愛,一旅行社對某小區居民在暑假期間去以上五個景區旅游(只選一個景區)的意向做了一次隨機調查統計,并根據這個統計結果制作了如下兩幅不完整的統計圖.
五個景區很受游客喜愛,一旅行社對某小區居民在暑假期間去以上五個景區旅游(只選一個景區)的意向做了一次隨機調查統計,并根據這個統計結果制作了如下兩幅不完整的統計圖.

![]() 該小區居民在這次隨機調查中被調查到的人數是_______人,
該小區居民在這次隨機調查中被調查到的人數是_______人, ![]() 想去
想去![]() 景區的人有_________人, 并補全條形統計圖.
景區的人有_________人, 并補全條形統計圖.
![]() 被調查到的居民想去 景區旅游的人數最多,若該小區有居民
被調查到的居民想去 景區旅游的人數最多,若該小區有居民![]() 人,估計去該景區旅游的居民約有多少人?
人,估計去該景區旅游的居民約有多少人?
![]() 小強同學贊假期間計劃與父母從
小強同學贊假期間計劃與父母從![]() 五個景區中,任選兩個去旅游,求選至
五個景區中,任選兩個去旅游,求選至![]() 兩個景區的概率,(要求列表求概率)
兩個景區的概率,(要求列表求概率)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com