
【題目】如圖,已知等腰三角形ABC的底角為30°,以BC為直徑的⊙O與底邊AB交于點D,過D作DE⊥AC,垂足為E.
(1)證明:DE為⊙O的切線;
(2)連接OE,若BC=4,求△OEC的面積.
【答案】
(1)證明:連接OD,CD,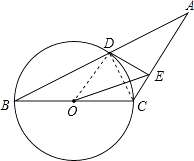
∵BC為⊙O直徑,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位線,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D點在⊙O上,
∴DE為⊙O的切線;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD= ![]() BC=2,BD=BCcos30°=2
BC=2,BD=BCcos30°=2 ![]() ,
,
∴AD=BD=2 ![]() ,AB=2BD=4
,AB=2BD=4 ![]() ,
,
∴S△ABC= ![]() ABCD=
ABCD= ![]() ×4
×4 ![]() ×2=4
×2=4 ![]() ,
,
∵DE⊥AC,
∴DE= ![]() AD=
AD= ![]() ×2
×2 ![]() =
= ![]() ,
,
AE=ADcos30°=3,
∴S△ODE= ![]() ODDE=
ODDE= ![]() ×2×
×2× ![]() =
= ![]() ,
,
S△ADE= ![]() AEDE=
AEDE= ![]() ×
× ![]() ×3=
×3= ![]() ,
,
∵S△BOD= ![]() S△BCD=
S△BCD= ![]() ×
× ![]() S△ABC=
S△ABC= ![]() ×4
×4 ![]() =
= ![]() ,
,
∴S△OEC=S△ABC-S△BOD-S△ODE-S△ADE=4 ![]() -
- ![]() -
- ![]() -
- ![]() =
= ![]() .
.
【解析】(1)連接OD,CD,由BC為⊙O的直徑,可得CD⊥AB,又由等腰三角形ABC的底角為30°,可得AD=BD,即可證得OD∥AC,進而可證得垂直,得出切線;(2)根據三角函數的定義,求得BD,DE,AE的長,然后求得△BOD,△ODE,△ADE以及△ABC的面積,進而求出面積.


科目:初中數學 來源: 題型:
【題目】如圖所示,長方形紙片ABCD的長AD=9cm,寬AB=3cm,將其折疊,使點D與點B重合.
求:(1)折疊后DE的長;(2)以折痕EF為邊的正方形面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
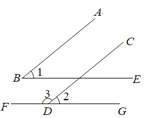
【題目】如圖,已知 AB∥CD,BE∥FG.
(1)如果∠1=53°,求∠2和∠3的度數;
(2)本題隱含著一個規律,請你根據(1)的結果進行歸納,如果一個角的兩邊分別平行于另一個角的兩邊,那么這兩個角__________;
(3)利用(2)的結論解答:如果兩個角的兩邊分別平行,其中一個角比另一個角的 2倍小 30°,求這兩個角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,過點B作BE⊥CD,垂足為E,連結AE.F為AE上一點,且∠BFE=∠C.
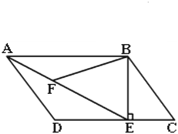
(1)ΔABF與ΔADE相似嗎?說說你的理由.
(2)若AB=4,∠BAE=30°,求AE的長.
(3)在(1)、(2)的條件下,若AD=3,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中描出下列各點,并將各組內的這些點依次用線段連接起來.

①![]() ,
,![]() ,
,![]() ;②
;②![]() ,
,![]() ,
,![]() ,
,![]() .
.
觀察所描出的圖形,解答下列問題:
(1)坐標軸上的點有_________,![]() 軸上的點_______坐標等于零,
軸上的點_______坐標等于零,![]() 軸上的點_____坐標等于零.
軸上的點_____坐標等于零.
(2)線段![]() 與
與![]() 軸_______,點
軸_______,點![]() 和點
和點![]() _______坐標相同,線段
_______坐標相同,線段![]() 上其他點_____坐標相同.
上其他點_____坐標相同.
(3)線段![]() 與
與![]() 軸_______,點
軸_______,點![]() 和點
和點![]() _______坐標相同,線段
_______坐標相同,線段![]() 上其他點_____坐標相同.
上其他點_____坐標相同.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索與拓展應用,
已知△ABC為等邊三角形,點D為直線BC上的一動點(點D不與B、C重合),以AD為邊作菱形ADEF(A、D、E、F按逆時針排列),使∠DAF=60°,連接CF.
(1)如圖1,當點D在邊BC上時,求證:①BD=CF;②AC=CF+CD;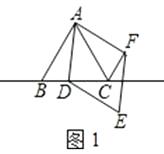
(2)如圖2,當點D在邊BC的延長線上且其他條件不變時,結論AC=CF+CD是否成立?若不成立,請寫出AC、CF、CD之間存在的數量關系,并說明理由;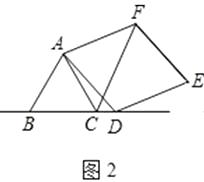
(3)如圖3,當點D在邊CB的延長線上且其他條件不變時,補全圖形,并直接寫出AC、CF、CD之間存在的數量關系.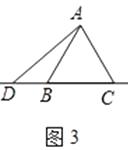
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家之一,2011年春季以來,我省遭受了嚴重的旱情,某校為了組織“節約用水從我做起”活動,隨機調查了本校120名同學家庭月人均用水量和節水措施情況,如圖1、圖2是根據調查結果做出的統計圖的一部分.
請根據信息解答下列問題:
(1)圖1中淘米水澆花所占的百分比為 ;
(2)圖1中安裝節水設備所在的扇形的圓心角度數為 ;
(3)補全圖2;
(4)如果全校學生家庭總人數為3000人,根據這120名同學家庭月人均用水量,估計全校學生家庭月用水總量是多少噸?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 上有
上有![]() 、
、![]() 兩點,
兩點,![]() ,點
,點![]() 是線段
是線段![]() 上的一點,OA=2OB.
上的一點,OA=2OB.
(1)![]() ________
________![]() ,
,![]() ________
________![]() ;
;
(2)若點C是線段AB上一點,且滿足![]() ,求CO的長;
,求CO的長;
(3)若動點![]() 、
、![]() 分別從點
分別從點![]() 、
、![]() 同時出發,在直線
同時出發,在直線![]() 上向右運動.點P的速度為
上向右運動.點P的速度為![]() ,點
,點![]() 的速度為
的速度為![]() ,設動點
,設動點![]() 、
、![]() 運動的時間為
運動的時間為![]() ,當點
,當點![]() 與點
與點![]() 重合時,
重合時,![]() 、
、![]() 兩點都停止運動,求當
兩點都停止運動,求當![]() 為何值時,
為何值時,![]() .
.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請填空,完成下面的證明,并注明理由.
如圖,![]() ,
,![]() ,BE平分
,BE平分![]() ,DF平分
,DF平分![]() .
.

求證:![]() .
.
證明:∵![]() ,(已知)
,(已知)
∴![]() .(_________)
.(_________)
∵![]() ,(已知)
,(已知)
∴__________![]() .(兩直線平行,同旁內角互補)
.(兩直線平行,同旁內角互補)
∴![]() .(_________)
.(_________)
∵![]() ,(已知)
,(已知)
∴![]() .(_________)
.(_________)
同理,![]() .
.
∴________=![]() .
.
∵![]() ,(已知)
,(已知)
∴![]() .(兩直線平行,內錯角相等)
.(兩直線平行,內錯角相等)
∴![]() .
.
∴![]() .(__________)
.(__________)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com