
【題目】在矩形ABCD中,BE平分∠ABC交CD邊于點(diǎn)E.點(diǎn)F在BC邊上,且FE⊥AE.
(1)如圖1,①∠BEC=_________°;
②在圖1已有的三角形中,找到一對(duì)全等的三角形,并證明你的結(jié)論;
(2)如圖2,F(xiàn)H∥CD交AD于點(diǎn)H,交BE于點(diǎn)M.NH∥BE,NB∥HE,連接NE.若AB=4,AH=2,求NE的長(zhǎng).

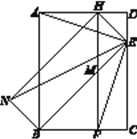
圖1 圖2
【答案】45
【解析】
(1)根據(jù)矩形的性質(zhì)得到![]() ,根據(jù)角平分線(xiàn)的定義得到
,根據(jù)角平分線(xiàn)的定義得到![]() ,根據(jù)三角形內(nèi)角和定理計(jì)算即可;
,根據(jù)三角形內(nèi)角和定理計(jì)算即可;
(2)利用![]() 定理證明
定理證明![]() ;
;
(3)連接![]() ,證明四邊形
,證明四邊形![]() 是矩形,得到
是矩形,得到![]() ,根據(jù)勾股定理求出
,根據(jù)勾股定理求出![]() 即可.
即可.
(1)①∵四邊形ABCD為矩形,
∴∠ABC=∠BCD=90°,
∵BE平分∠ABC,
∴∠EBC=45°,
∴∠BEC=45°,
故答案為:45;
②△ADE≌△ECF,
理由如下:∵四邊形ABCD是矩形,
∴∠ABC=∠C=∠D=90°,AD=BC.
∵FE⊥AE,
∴∠AEF=90°.
∴∠AED+∠FEC=180°-∠AEF=90°.
∵∠AED+∠DAE=90°,
∴∠FEC=∠EAD,
∵BE平分∠ABC,
![]()
∴∠BEC=45°.
∴∠EBC=∠BEC.
∴BC=EC.
∴AD=EC.
在△ADE和△ECF中,
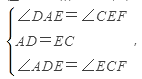
∴△ADE≌△ECF;
(2)連接HB,如圖2,
∵FH∥CD,
∴∠HFC=180°-∠C=90°.
∴四邊形HFCD是矩形.
∴DH=CF,
∵△ADE≌△ECF,
∴DE=CF.
∴DH=DE.
∴∠DHE=∠DEH=45°.
∵∠BEC=45°,
∴∠HEB=180°-∠DEH-∠BEC=90°.
∵NH∥BE,NB∥HE,
∴四邊形NBEH是平行四邊形.
∴四邊形NBEH是矩形.
∴NE=BH.
∵四邊形ABCD是矩形,
∴∠BAH=90°.
∵在Rt△BAH中,AB=4,AH=2,



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校要從甲、乙、丙、丁四名學(xué)生中選一名參加“漢字聽(tīng)寫(xiě)”大賽,選拔中每名學(xué)生的平均成績(jī) ![]() 及其方差s2如表所示,如果要選拔一名成績(jī)高且發(fā)揮穩(wěn)定的學(xué)生參賽,則應(yīng)選擇的學(xué)生是( )
及其方差s2如表所示,如果要選拔一名成績(jī)高且發(fā)揮穩(wěn)定的學(xué)生參賽,則應(yīng)選擇的學(xué)生是( )
甲 | 乙 | 丙 | 丁 | |
| 8.9 | 9.5 | 9.5 | 8.9 |
s2 | 0.92 | 0.92 | 1.01 | 1.03 |
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知關(guān)于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求證:此方程總有兩個(gè)實(shí)數(shù)根;
(2)若此方程有一個(gè)根大于0且小于1,求k的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知原點(diǎn)O,A(0,4),B(2,0),將△OAB繞平面內(nèi)一點(diǎn)P逆時(shí)針旋轉(zhuǎn)90°,使得旋轉(zhuǎn)后的三角形的兩個(gè)頂點(diǎn)恰好落在雙曲線(xiàn) ![]() 上,則旋轉(zhuǎn)中心P的坐標(biāo)為。
上,則旋轉(zhuǎn)中心P的坐標(biāo)為。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知?jiǎng)狱c(diǎn)P以每秒2㎝的速度沿圖甲的邊框按從![]() 的路徑移動(dòng),相應(yīng)的△ABP的面積S關(guān)于時(shí)間t的函數(shù)圖象如圖乙.若AB=6,試回答下列問(wèn)題:
的路徑移動(dòng),相應(yīng)的△ABP的面積S關(guān)于時(shí)間t的函數(shù)圖象如圖乙.若AB=6,試回答下列問(wèn)題:

(1)圖甲中的BC長(zhǎng)是多少?
(2)圖乙中的a是多少?
(3)圖甲中的圖形面積的多少?
(4)圖乙的b是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,將腰CD以點(diǎn)D為中心逆時(shí)針旋轉(zhuǎn)90°至ED,連結(jié)AE,CE,則△ADE的面積是( ) 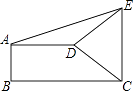
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在△ABC外作△ABD和△ACE,使AD=AB,AE=AC,且∠DAB=∠EAC,連接BE,CD相交于P點(diǎn),求證:點(diǎn)A在∠DPE的平分線(xiàn)上.
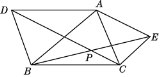
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)算或化簡(jiǎn)
(1)計(jì)算﹣14﹣(1﹣0.5)×![]() .
.
(2)計(jì)算(![]() )×(﹣36)+1+(﹣2)+|﹣2﹣3|﹣5.
)×(﹣36)+1+(﹣2)+|﹣2﹣3|﹣5.
(3)化簡(jiǎn)(3a﹣2b)+(5a﹣7b)﹣2(2a﹣4b).
(4)化簡(jiǎn)(﹣x2+2xy﹣y2)﹣2(xy﹣3x2)+3(2y2﹣xy).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com