
【題目】六年級(1)班從學校出發,乘大巴車去農場進行實踐活動,之后返回學校(大巴車行駛速度不變),下圖反映的是大巴車行駛路程與時間之間的關系。請同學們觀察圖象,進行數據分析,求大巴車離開學校多少小時時,大巴車與農場相距![]() 。
。

【答案】大巴車離開學校后![]() 小時或
小時或![]() 小時時與農場相距
小時時與農場相距![]() .
.
【解析】
圖中反應的行駛的路程和時間的關系,有圖可知,0~1小時之間時,大巴車出發去農場,1~3小時之間,大巴車已經到了農場未動,此時正在參與實踐過程,3~4小時之間,大巴車出發返回學校.所以大巴車與農場相距![]() 的時刻有兩處,分別是出發去農場時和返程回學校時.
的時刻有兩處,分別是出發去農場時和返程回學校時.
由圖象可知:出發1小時,對應著大巴車已到了農場,學校與農場相距![]() ,所以大巴車的速度為40千米/小時,往返過程中都存在大巴車與農場相距10千米的情況。
,所以大巴車的速度為40千米/小時,往返過程中都存在大巴車與農場相距10千米的情況。
去時:大巴車離開學校行駛30km時,距離農場10km.
則用時為30÷40=![]() 小時
小時
返回時:大巴車只要行駛10km時,距離農場10km.
則用時為10÷40=![]() 小時,又因為題中問的是大巴車離開學校多少小時時,距離農場10km
小時,又因為題中問的是大巴車離開學校多少小時時,距離農場10km
所以用時為![]() +3=
+3=![]() 小時
小時
故答案為:大巴車離開學校后![]() 小時或
小時或![]() 小時時與農場相距
小時時與農場相距![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,直線l1的表達式為:y=-3x+3,且直線l1與x軸交于點D,直線l2經過點A,B,直線l1,l2交于點C.
(1)求點D的坐標;
(2)求直線l2的解析表達式;
(3)求△ADC的面積;
(4)在直線l2上存在異于點C的另一點P,使得△ADP與△ADC的面積相等,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
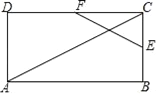
【題目】如圖,在矩形ABCD中,已知AB=24,BC=12,點E沿BC邊從點B開始向點C以每秒2個單位長度的速度運動;點F沿CD邊從點C開始向點D以每秒4個單位長度的速度運動,如果E、F同時出發,用t(0≤t≤6)秒表示運動的時間,當t為何值時,以點E、C、F為頂點的三角形與△ACD相似?
查看答案和解析>>
科目:初中數學 來源: 題型:
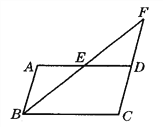
【題目】如圖,平行四邊形ABCD中,點E是AD的中點,BE的延長線與CD的延長線交于點F.
(1)求證:△ABE≌△DFE;
(2)試連結BD,AF,判斷四邊形ABDF的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y=kx+4(k≠0)與y軸交于點A.
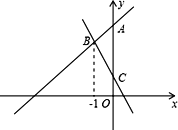
(1)如圖,直線y=﹣2x+1與直線y=kx+4(k≠0)交于點B,與y軸交于點C,點B的橫坐標為-1.
①求點B的坐標及k的值;
②直線y=﹣2x+1與直線y=kx+4與y軸所圍成的△ABC的面積等于 ;
(2)直線y=kx+4(k≠0)與x軸交于點E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
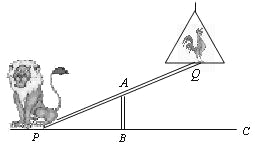
【題目】如圖,馬戲團讓獅子和公雞表演蹺蹺板節目.蹺蹺板支柱 AB的高度為1.2米.
(1)若吊環高度為2米,支點 A為蹺蹺板 PQ的中點,獅子能否將公雞送到吊環上?為什么?
(2)若吊環高度為3.6米,在不改變其他條件的前提下移動支柱,當支點 A移到蹺蹺板 PQ的什么位置時,獅子剛好能將公雞送到吊環上?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1955年,印度數學家卡普耶卡(![]() )研究了對四位自然數的一種變換:任給出四位數
)研究了對四位自然數的一種變換:任給出四位數![]() ,用
,用![]() 的四個數字由大到小重新排列成一個四位數
的四個數字由大到小重新排列成一個四位數![]() ,再減去它的反序數
,再減去它的反序數![]() (即將
(即將![]() 的四個數字由小到大排列,規定反序后若左邊數字有0,則將0去掉運算,比如0001,計算時按1計算),得出數
的四個數字由小到大排列,規定反序后若左邊數字有0,則將0去掉運算,比如0001,計算時按1計算),得出數![]() ,然后繼續對
,然后繼續對![]() 重復上述變換,得數
重復上述變換,得數![]() ,…,如此進行下去,卡普耶卡發現,無論
,…,如此進行下去,卡普耶卡發現,無論![]() 是多大的四位數,只要四個數字不全相同,最多進行
是多大的四位數,只要四個數字不全相同,最多進行![]() 次上述變換,就會出現變換前后相同的四位數
次上述變換,就會出現變換前后相同的四位數![]() ,這個數稱為
,這個數稱為![]() 變換的核.則四位數9631的
變換的核.則四位數9631的![]() 變換的核為______.
變換的核為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,![]() 的頂點均在格點上,
的頂點均在格點上,![]() ,
,![]() 也在格點上.
也在格點上.

(1)畫出![]() 先向右平移5個單位長度,再向下平移5個單位長度得到的
先向右平移5個單位長度,再向下平移5個單位長度得到的![]() ;
;
(2)畫出![]() 關于直線
關于直線![]() 對稱的
對稱的![]() ;
;
(3)畫出![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 后所得的
后所得的![]() ;
;
(4)![]() 與
與![]() 組成的圖形是軸對稱圖形嗎?如果是軸對稱圖形,請畫出對稱軸.
組成的圖形是軸對稱圖形嗎?如果是軸對稱圖形,請畫出對稱軸.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com