
【題目】“格子乘法”是15世紀中葉,意大利數學家帕喬利在《算術幾何及比例性質摘要》一書中介紹的一種兩個數的相乘的計算方法.這種方法傳入中國之后,在明朝數學家程大位的《算法統(tǒng)宗》書中被稱為“鋪地錦”具體步驟如下:
①先畫一個矩形,把它分成p×q個方格(p,q分別為兩乘數的位數)在方格上邊、右邊分別寫下兩個因數;
②再用對角線把方格一分為二,分別記錄上述各位數字相應乘積的十位數與個位數;
③然后這些乘積由右下到左上,沿對角線方向相加,相加滿十時向前進一;
④最后得到結果(方格左側與下方數字依次排列).比如:
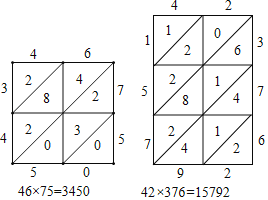
(1)圖1是用“鋪地錦”計算x9×784的格子,則z= ,x9×784=
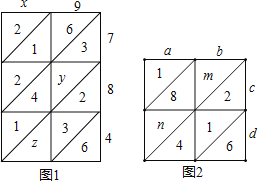
(2)圖2是用“鋪地錦”計算ab×cd的格子,已知ab×cd=2176,求m和n的值.
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() .點P第1次向右平移1個單位長度,向下平移2個單位長度至點
.點P第1次向右平移1個單位長度,向下平移2個單位長度至點![]() ,接著,第2次向右平移1個單位長度,向上平移3個單位長度至點
,接著,第2次向右平移1個單位長度,向上平移3個單位長度至點![]() ,第3次向右平移1個單位長度,向下平移4個單位長度至點
,第3次向右平移1個單位長度,向下平移4個單位長度至點![]() ,第4次向右平移1個單位長度,向上平移5個單位至點
,第4次向右平移1個單位長度,向上平移5個單位至點![]() ,…,按照此規(guī)律,點
,…,按照此規(guī)律,點![]() 第2019次平移至點
第2019次平移至點![]() 的坐標是
的坐標是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:將邊長為![]() 的正三角形的三條邊分別
的正三角形的三條邊分別![]() 等分,連接各邊對應的等分點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
等分,連接各邊對應的等分點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
探究:要研究上面的問題,我們不妨先從最簡單的情形入手,進而找到一般性規(guī)律.
探究一:將邊長為2的正三角形的三條邊分別二等分,連接各邊中點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
如圖①,連接邊長為2的正三角形三條邊的中點,從上往下看:
邊長為1的正三角形,第一層有1個,第二層有3個,共有![]() 個;
個;
邊長為2的正三角形一共有1個.

探究二:將邊長為3的正三角形的三條邊分別三等分,連接各邊對應的等分點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
如圖②,連接邊長為3的正三角形三條邊的對應三等分點,從上往下看:邊長為1的正三角形,第一層有1個,第二層有3個,第三層有5個,共有![]() 個;邊長為2的正三角形共有
個;邊長為2的正三角形共有![]() 個.
個.

探究三:將邊長為4的正三角形的三條邊分別四等分(圖③),連接各邊對應的等分點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
(仿照上述方法,寫出探究過程)

結論:將邊長為![]() 的正三角形的三條邊分別
的正三角形的三條邊分別![]() 等分,連接各邊對應的等分點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
等分,連接各邊對應的等分點,則該三角形中邊長為1的正三角形和邊長為2的正三角形分別有多少個?
(仿照上述方法,寫出探究過程)
應用:將一個邊長為25的正三角形的三條邊分別25等分,連接各邊對應的等分點,則該三角形中邊長為1的正三角形有______個和邊長為2的正三角形有______個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某種車的耗油量,我們對這種車做了試驗,并把試驗的數據記錄下來,制成下表:
汽車行駛時間t(h) | 0 | 1 | 2 | 3 | ······ |
剩余油量Q(L) | 50 | 44 | 38 | 32 | ······ |
(1)根據上表的數據,能用t表示Q嗎?試一試;
(2)汽車行駛5h后,油箱中的剩余油量是多少?
(3)若汽車油箱中剩余油量為14L,則汽車行使了多少小時?
(4)貯滿50L汽油的汽車,最多行駛幾小時?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】西南大學銀翔實驗中學第二屆繽紛科技節(jié)于2019年5月份隆重舉行,主題:綠色體驗成長﹣玩出你的稀缺競爭力,本屆繽紛科技節(jié)有展示類、體驗類、競賽類共40多個項目.4月份,學校對活動中所需物品統(tǒng)一購,其中某一體驗類項目需要A、B兩種材料,已知A種材料單價32元/套,B種材料單價24元/套,活動需要A、B兩種材料共50套計劃購買A、B兩種材料總費用不超過1392元.
(1)若按計劃采購,最多能購買A種材料多少套?
(2)在實際來購過程中,受多方面因素的影響,與(1)中最多購買A種材料的計劃相比,實際采購A種材料數量的增加了![]() a%,B種材料的數量減少
a%,B種材料的數量減少![]() a%(A、B材料的數量均為整數),實際采購A種材料的單價減少了
a%(A、B材料的數量均為整數),實際采購A種材料的單價減少了![]() a%,B種材料的單價增加
a%,B種材料的單價增加![]() a%,且實際總費用比按(1)中最多購買A種材料的總費用多了16元,求a.
a%,且實際總費用比按(1)中最多購買A種材料的總費用多了16元,求a.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CA⊥AB,DB⊥AB,已知AC=2,AB=6,點P射線BD上一動點,以CP為直徑作⊙O,點P運動時,若⊙O與線段AB有公共點,則BP最大值為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
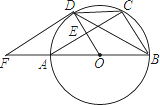
【題目】如圖,AB是⊙O的直徑,AC是弦,半徑OD⊥AC于點E,過點D的切線與BA延長線交于點F.
(1)求證:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小文同學統(tǒng)計了他所在小區(qū)居民每天微信閱讀的時間,并繪制了直方圖.有以下說法:①小文同學一共統(tǒng)計了60人;②每天微信閱讀不足20分鐘的人數有8人;③每天微信閱讀30~40分鐘的人數最多;④每天微信閱讀0-10分鐘的人數最少.根據圖中信息,上述說法中正確的是( )

A. ①②③④ B. ①②③ C. ②③④ D. ③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,直線y=﹣x﹣3與x軸交于點A,與y軸交于點C,拋物線y=x2+bx+c經過A、C兩點,與x軸交于另一點B
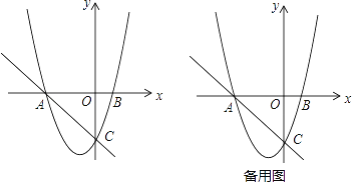
(1)求拋物線的解析式;
(2)點D是第二象限拋物線上的一個動點,連接AD、BD、CD,當S△ACD=![]() S四邊形ACBD時,求D點坐標;
S四邊形ACBD時,求D點坐標;
(3)在(2)的條件下,連接BC,過點D作DE⊥BC,交CB的延長線于點E,點P是第三象限拋物線上的一個動點,點P關于點B的對稱點為點Q,連接QE,延長QE與拋物線在A、D之間的部分交于一點F,當∠DEF+∠BPC=∠DBE時,求EF的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com