
【題目】(2016山西省)我省某蘋果基地銷售優質蘋果,該基地對需要送貨且購買量在2000kg﹣5000kg(含2000kg和5000kg)的客戶有兩種銷售方案(客戶只能選擇其中一種方案):
方案A:每千克5.8元,由基地免費送貨.
方案B:每千克5元,客戶需支付運費2000元.
(1)請分別寫出按方案A,方案B購買這種蘋果的應付款y(元)與購買量x(kg)之間的函數表達式;
(2)求購買量x在什么范圍時,選用方案A比方案B付款少;
(3)某水果批發商計劃用20000元,選用這兩種方案中的一種,購買盡可能多的這種蘋果,請直接寫出他應選擇哪種方案.

科目:初中數學 來源: 題型:
【題目】已知:![]() ,OB,OM,ON是
,OB,OM,ON是![]() 內的射線.
內的射線.
![]() 如圖1,若OM平分
如圖1,若OM平分![]() ,ON平分
,ON平分![]() 當射線OB繞點O在
當射線OB繞點O在![]() 內旋轉時,
內旋轉時,![]() ______度
______度![]()
![]() 也是
也是![]() 內的射線,如圖2,若
內的射線,如圖2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,當
,當![]() 繞點O在
繞點O在![]() 內旋轉時,求
內旋轉時,求![]() 的大小.
的大小.
![]() 在
在![]() 的條件下,若
的條件下,若![]() ,當
,當![]() 在
在![]() 繞O點以每秒
繞O點以每秒![]() 的速度逆時針旋轉t秒,如圖3,若
的速度逆時針旋轉t秒,如圖3,若![]() :
:![]() :3,求t的值.
:3,求t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
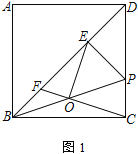
【題目】已知:在正方形ABCD中,AB=6,P為邊CD上一點,過P點作PE⊥BD于點E,連接BP.
(1)O為BP的中點,連接CO并延長交BD于點F
①如圖1,連接OE,求證:OE⊥OC;
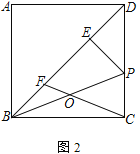
②如圖2,若![]() ,求DP的長;
,求DP的長;
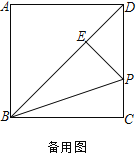
(2)![]() =___________
=___________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A,B,C,D四個點不在同一直線上,根據下列語句畫圖.
(1)畫射線AB,畫直線AC,畫線段AD;
(2)連接BD與直線AC相交于點E;
(3)延長線段BC,反向延長線段DC;
(4)若在上述所畫的圖形中,設從點D到點C有四條路徑,它們分別是①D→A→B→C;②D→B→C;③D→E→C;④D→C;哪條道路最短?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
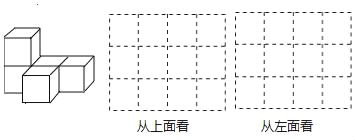
【題目】由大小相同的小立方塊搭成的幾何體如左圖:
(1)請在下面的方格中畫出該幾何體從上面和從左面看的兩個圖形.
(2)若現在你手頭上還有一些相同的小立方塊,如果保持從上面看和從左面看所得圖形不變,則在左圖中最多可以再添加 個小立方塊.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)若關于x的方程2x﹣3=1和![]() =k﹣3x有相同的解,求k的值
=k﹣3x有相同的解,求k的值
(2)閱讀材料:解方程組![]() 時,可由①得x﹣y=1③,然后再將③代入②得4×1﹣y=5,求得y=﹣1,從而進一步求得
時,可由①得x﹣y=1③,然后再將③代入②得4×1﹣y=5,求得y=﹣1,從而進一步求得![]() ,這種方法被稱為“整體代入法”,請用上述方法解方程組
,這種方法被稱為“整體代入法”,請用上述方法解方程組 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y=ax2+bx﹣4(a≠0)的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸交于點C.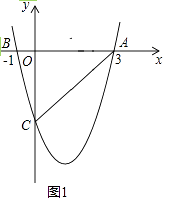
(1)求該二次函數的解析式及點C的坐標;
(2)設該拋物線的頂點為D,求△ACD的面積;
(3)若點P,Q同時從A點出發,如圖2(注:圖2與圖1完全相同),都以每秒1個單位長度的速度分別沿線段AB,AC運動,當其中一點到達終點時,另一點也隨之停止運動,當P,Q運動到t秒時,將△APQ沿PQ所在直線翻折,點A恰好落在拋物線上E處,判定此時四邊形APEQ的形狀,說明理由,并求出點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某路公交車從起點經過A、B、C、D站到達終點,一路上下乘客如下表所示。(用正數表示上車的人數,負數表示下車的人數)

(1)到終點下車還有________人.
(2)車行駛在那兩站之間車上的乘客最多?________站和________站
(3)若每人乘坐一站需買票1元,問該車出車一次能收入多少錢?寫出算式。
查看答案和解析>>
科目:初中數學 來源: 題型:
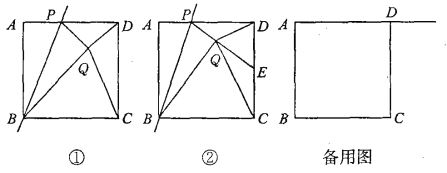
【題目】如圖①,已知正方形ABCD的邊長為1,點P是AD邊上的一個動點,點A關于直線BP的對稱點是點Q,連接PQ、DQ、CQ、BQ,設AP=x.
(1)BQ+DQ的最小值是_______,此時x的值是_______;
(2)如圖②,若PQ的延長線交CD邊于點E,并且∠CQD=90°.
①求證:點E是CD的中點; ②求x的值.
(3)若點P是射線AD上的一個動點,請直接寫出當△CDQ為等腰三角形時x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com