
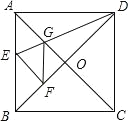
【題目】如圖,在正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合,展開后,折疊DE分別交AB、AC于E、G,連接GF,下列結論:①∠FGD=112.5°②BE=2OG③S△AGD=S△OGD④四邊形AEFG是菱形( )
A. 1個B. 2個C. 3個D. 4個
【答案】C
【解析】
①由四邊形ABCD是正方形和折疊性得出∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,再由三角形的內角和求出∠FGD=112.5°.故①正確,
②④由四邊形ABCD是正方形和折疊,判斷出四邊形AEFG是平行四邊形,再由AE=EF,得出四邊形AEFG是菱形.利用45°的直角三角形得出GF=![]() OG,BE=
OG,BE=![]() EF=
EF=![]() GF,得出BE=2OG,故②④正確.
GF,得出BE=2OG,故②④正確.
③由四邊形ABCD是正方形和折疊性,得到△ADG≌△FDG,所以S△AGD=S△FDG≠S△OGD故③錯誤.
①由四邊形ABCD是正方形和折疊性知,
∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,
∴∠FGD=180°﹣∠DFG﹣∠FDG=180°﹣45°﹣22.5°=112.5°,
故①正確,
②由四邊形ABCD是正方形和折疊性得出,
∠DAG=∠DFG=45°,∠EAD=∠EFD=90°,AE=EF,
∵∠ABF=45°,
∴∠ABF=∠DFG,
∴AB∥GF,
又∵∠BAC=∠BEF=45°,
∴EF∥AC,
∴四邊形AEFG是平行四邊形,
∴四邊形AEFG是菱形.
∵在Rt△GFO中,GF=![]() OG,
OG,
在Rt△BFE中,BE=![]() EF=
EF=![]() GF,
GF,
∴BE=2OG,
故②④正確.
③由四邊形ABCD是正方形和折疊性知,
AD=FD,AG=FG,DG=DG,
在△ADG和△FDG中,
 ,
,
∴△ADG≌△FDG(SSS),
∴S△AGD=S△FDG≠S△OGD
故③錯誤.
正確的有①②④,
故選C.


科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
壹娛觀察分析![]() -
-![]() 中國內地四年春節檔及節后的三個自然周(下文簡稱“節后三周”)的票房表現.
中國內地四年春節檔及節后的三個自然周(下文簡稱“節后三周”)的票房表現.
從柱狀圖變化趨勢中,可以看出![]() 年-
年-![]() 年春節檔和節后三周票房,都有著連續的高速增長.在
年春節檔和節后三周票房,都有著連續的高速增長.在![]() 年,春節檔、節后三周票房分別是
年,春節檔、節后三周票房分別是![]() 億元和
億元和![]() 億元,同
億元,同![]() 年增長率分別達到
年增長率分別達到![]() 和
和![]() .
.
這一迅猛的勢頭在![]() 年被打斷,春節檔和節后票房增長率分別跌至
年被打斷,春節檔和節后票房增長率分別跌至![]() 、
、![]() .如果去除自
.如果去除自![]() 年開始計入票價的
年開始計入票價的![]() 左右的服務費,增幅還將進一步縮窄.
左右的服務費,增幅還將進一步縮窄.
相比于![]() 年春節檔的同比增速
年春節檔的同比增速![]() ,
, ![]() 節后三周
節后三周![]() 的同比增速要稍好看一些,而且是最近三年來第一次節后三周同比增幅高于春節檔同比增幅.
的同比增速要稍好看一些,而且是最近三年來第一次節后三周同比增幅高于春節檔同比增幅.
在萬達![]() 年業績快報中,曾提到“由于新建影院大多數位于三四線城市,以及受新開影院上座率低的拖累,公司的場均人次有所下滑,同比下降
年業績快報中,曾提到“由于新建影院大多數位于三四線城市,以及受新開影院上座率低的拖累,公司的場均人次有所下滑,同比下降![]() ”從這一闡述中,我們可以窺見三四線城市電影市場,在增長上的短板.
”從這一闡述中,我們可以窺見三四線城市電影市場,在增長上的短板.
根據以上材料解答下列問題:
(![]() )
)![]() 年中國內地春節周票房收入為__________億元,節后三周票房收入__________億元.
年中國內地春節周票房收入為__________億元,節后三周票房收入__________億元.
(![]() )若
)若![]()
![]() ,則春節檔引進片電影票房為__________億
,則春節檔引進片電影票房為__________億
元.
(![]() )請用統計表將
)請用統計表將![]() -
-![]() 年中國內地春節周票房和節后三周票房成績表示出來.
年中國內地春節周票房和節后三周票房成績表示出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上原點左邊有一點A,點A對應著數a,有如下說法:
①﹣a表示的數一定是一個正數.
②若|a|=9時,則a=﹣9.
③在﹣a,![]() ,a2,a3中,最大的數值是a2.
,a2,a3中,最大的數值是a2.
④式子|a+![]() |的最小值為2.
|的最小值為2.
其中正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
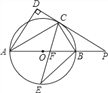
【題目】如圖,AB是⊙O的直徑,點C是⊙O上一點,AD和過點C的切線互相垂直,垂足為D,直線DC與AB的延長線相交于P.弦CE平分∠ACB,交直徑AB于點F,連結BE.
(1)求證:AC平分∠DAB;
(2)探究線段PC,PF之間的大小關系,并加以證明;
(3)若tan∠PCB=![]() ,BE=
,BE=![]() ,求PF的長.
,求PF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一張足夠大的紙板上截取一個面積為![]() 的矩形紙板
的矩形紙板![]() ,如圖
,如圖![]() ,再在矩形紙板的四個角上切去邊長相等的小正方形,再把它的邊沿虛線折起,做成一個無蓋的長方體紙盒,底面
,再在矩形紙板的四個角上切去邊長相等的小正方形,再把它的邊沿虛線折起,做成一個無蓋的長方體紙盒,底面![]() 為矩形,如圖
為矩形,如圖![]() ,設小正方形的邊長為
,設小正方形的邊長為![]() 厘米.、
厘米.、
(1)若矩形紙板的一個邊長為![]() .
.
①當紙盒的底面積為![]() 時,求
時,求![]() 的值;
的值;
②求紙盒的側面積的最大值;
(2)當![]() ,且側面積與底面積之比為
,且側面積與底面積之比為![]() 時,求
時,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
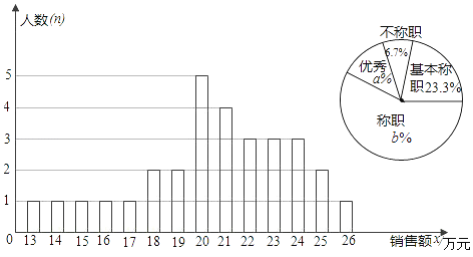
【題目】某商場統計了每個營業員在某月的銷售額,繪制了如下的條形統計圖以及不完整的扇形統計圖:
解答下列問題:
(1)設營業員的月銷售額為x(單位:萬元),商場規定:當x<15時為不稱職,當15≤x<20時,為基本稱職,當20≤x<25為稱職,當x≥25時為優秀.則扇形統計圖中的a=________,b=________.
(2)所有營業員月銷售額的中位數和眾數分別是多少?
(3)為了調動營業員的積極性,決定制定一個月銷售額獎勵標準,凡到達或超過這個標準的營業員將受到獎勵.如果要使得營業員的半數左右能獲獎,獎勵標準應定為多少萬元?并簡述其理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求畫圖
(1)如圖,平面上有五個點A,B,C,D,E. 按下列要求畫出圖形.
①連接BD;
②畫直線AC交BD于點M;
③過點A作線段AP⊥BD于點P;
④請在直線AC上確定一點N,使B,E兩點到點N的距離之和最小(保留作圖痕跡).
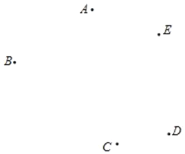
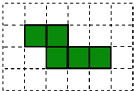
(2)小強用5個大小一樣的正方形制成如圖所示的拼接圖形(陰影部分),請你在圖中的拼接圖形上再接一個正方形,使新拼接成的圖形經過折疊后能成為一個封閉的正方體盒子.注意:只需添加一個符合要求的正方形,并用陰影表示.
查看答案和解析>>
科目:初中數學 來源: 題型:
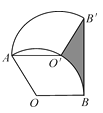
【題目】如圖,將半徑為2,圓心角為120°的扇形OAB繞點A逆時針旋轉60°,點O,B的對應點分別為O′,B′,連接BB′,則圖中陰影部分的面積是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com