
(本題6分)如圖所示,在⊙O中,  =
=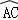 ,弦AB與弦AC交于點A,弦CD與AB交于點F,連接BC.
,弦AB與弦AC交于點A,弦CD與AB交于點F,連接BC.

(1)求證:AC2=ABAF;
(2)若⊙O的半徑長為2cm,∠B=60°,求圖中陰影部分面積.
(1)證明詳見解析;(2) .
.
【解析】
試題分析:(1)由等弧所對的圓周角相等得到一對角相等,再由一對公共角相等,可以得出△ACF∽△ABC,應用相似三角形的性質證得結論;
(2)連接OA,OC,利用同弧所對的圓心角等于圓周角的2倍,求出∠AOC=120°,過O作OE⊥AC,垂足為E,利用等腰三角形的三線合一得到∠AOE=60°,在Rt△AOE中,求出OE=1cm,AE=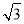 cm,進而求出AC=2
cm,進而求出AC=2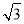 cm,由扇形AOC的面積減去△AOC的面積表示出陰影部分的面積.
cm,由扇形AOC的面積減去△AOC的面積表示出陰影部分的面積.
試題解析:【解析】
(1)證明:∵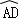 =
=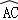 ,∴∠ACD=∠ABC,又∠BAC=∠CAF,∴△ACF∽△ABC,
,∴∠ACD=∠ABC,又∠BAC=∠CAF,∴△ACF∽△ABC,
∴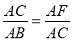 ,即AC2=ABAF;
,即AC2=ABAF;
(2)【解析】
連接OA,OC,過O作OE⊥AC,垂足為點E,
∵∠ABC=60°,∴∠AOC=120°,
又OA=OC,∴∠AOE=∠COE=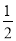 ×120°=60°,
×120°=60°,
在Rt△AOE中,OA=2cm,∴OE=OAcos60°=1cm,
∴AE= cm,
cm,
∴AC=2AE=2 cm,
cm,
則S陰影=S扇形OAC﹣S△AOC=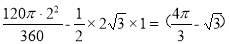 cm2.
cm2.

考點:相似三角形的判定和性質;扇形的面積公式;圓心角、弧、弦的關系;圓周角定理.
考點分析: 考點1:圓 圓,圓的有關性質與圓的有關計算是近幾年各地中考命題的重點內容。題型以填空題,選擇題和解答題為主,也有以閱讀理解,條件開放,結論開放探索題作為新的題型,分值一般是6-12分,難易度為中,考察內容:①圓的有關性質的應用。垂徑定理是重點。② 直線和圓,圓和圓的位置關系的判定及應用。③弧長,扇形面積,圓柱,圓錐的側面積和全面積的計算④圓與相似三角形,三角函數的綜合運用以及有關的開放題,探索題。突破方法:①熟練掌握圓的有關行政,掌握求線段,角的方法,理解概念之間的相互聯系和知識之間的相互轉化。②理解直線和原的三種位置關系,掌握切線的性質和判定的歌,會根據條件解決圓中的動態問題。③掌握有兩圓半徑的和或差與圓心距的大小關系來盤底的那個兩個圓的位置關系,對中考試題中常出現的閱讀理解題,探索題,要靈活運用圓的有關性質,進行合理推理與計算。④掌握弧長,扇形面積計算公式。⑤理解圓柱,圓錐的側面展開圖⑥對組合圖形 的計算要靈活運用計算方法解題。 試題屬性

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數學 來源:2014-2015學年四川省巴中市平昌縣九年級下學期第一次綜合性階段考試數學試卷(解析版) 題型:解答題
(10分)如圖,已知反比例函數 (k1>0)與一次函數
(k1>0)與一次函數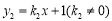 相交于A、B兩點,AC⊥x軸于點C.若△OAC的面積為1,且tan∠AOC=2 .
相交于A、B兩點,AC⊥x軸于點C.若△OAC的面積為1,且tan∠AOC=2 .

(1)求出反比例函數與一次函數的解析式;
(2)請直接寫出B點的坐標,并指出當x為何值時,反比例函數y1的值大于一次函數y2的值?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省巴中市平昌縣九年級下學期第一次綜合性階段考試數學試卷(解析版) 題型:選擇題
下列各式計算正確的是( ).
A.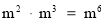
B.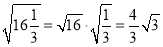
C.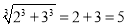
D. (a<1)
(a<1)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省棗莊市九年級3月測試數學試卷(解析版) 題型:解答題
(本題12分)如圖,在平面直角坐標系中,已知OA=2,OC=4,⊙M與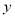 軸相切于點C,與
軸相切于點C,與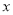 軸交于A,B兩點,∠ACD=90°,拋物線
軸交于A,B兩點,∠ACD=90°,拋物線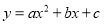 經過A,B,C三點.
經過A,B,C三點.
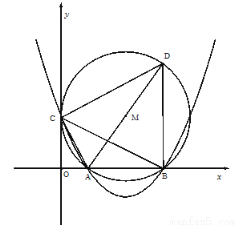
(1)求證:∠CAO=∠CAD;
(2)求弦BD的長;
(3)在拋物線的對稱軸上是否存在點P使ΔPBC是以BC為腰的等腰三角形?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省棗莊市九年級3月測試數學試卷(解析版) 題型:填空題
小明在某風景區的觀景臺O處觀測到東北方向的P處有一艘貨船, 該船正向南勻速航 行,30分鐘后再觀察時,該船已航行到O的南偏東30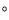 ,且與O相距6km的Q處.如圖所示.貨船的航行速度是____________km/h.(結果用根號表示.)
,且與O相距6km的Q處.如圖所示.貨船的航行速度是____________km/h.(結果用根號表示.)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省棗莊市九年級3月測試數學試卷(解析版) 題型:選擇題
已知關于 的方程
的方程 ,下列說法正確的是( ).
,下列說法正確的是( ).
A.當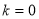 時,方程無解
時,方程無解
B.當 時,方程有兩個相等的實數解
時,方程有兩個相等的實數解
C.當 時,方程有一個實數解
時,方程有一個實數解
D.當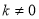 時,方程總有兩個不相等的實數解
時,方程總有兩個不相等的實數解
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省學業水平模擬考試數學試卷(解析版) 題型:填空題
如圖,已知正方形ABCD的邊長為3,E為CD邊上一點,DE=1.以點A為中心,把△ADE順時針旋轉90°,得△ABE′,連接EE′,則EE′的長等于_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com