
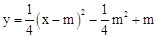 的頂點為A,與y軸的交點為B,連結AB,AC⊥AB,交y軸于點C,延長CA到點D,使AD=AC,連結BD.作AE∥x軸,DE∥y軸.
的頂點為A,與y軸的交點為B,連結AB,AC⊥AB,交y軸于點C,延長CA到點D,使AD=AC,連結BD.作AE∥x軸,DE∥y軸.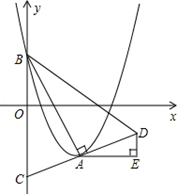
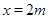 ,
,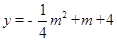 ,將
,將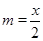 代入
代入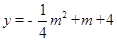 ,即可求出二次函數(shù)的表達式;
,即可求出二次函數(shù)的表達式; (x-2)2+1,
(x-2)2+1, (x-2)2+1,得:y=2,
(x-2)2+1,得:y=2, m2+m),點B(0,m),
m2+m),點B(0,m), m2+m)=
m2+m)= m2,
m2,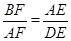 ,
,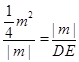 ,
, m2+m),
m2+m), m2+m+4),
m2+m+4), m2+m+4,
m2+m+4, •(
•(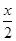 )2+
)2+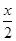 +4,
+4, x2+
x2+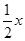 +4,
+4,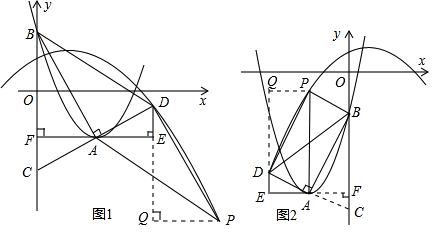
 m2+m+4)-(
m2+m+4)-( m2)=-
m2)=- m2+m+4,
m2+m+4, m2+m+4)的坐標代入y=-
m2+m+4)的坐標代入y=- x2+
x2+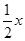 +4得:-
+4得:- m2+m+4=-
m2+m+4=- ×(3m)2+
×(3m)2+ ×(3m)+4,
×(3m)+4, m2+m+4)+(
m2+m+4)+( m2)=m+4,
m2)=m+4, x2+
x2+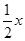 +4得:
+4得: m2+
m2+ m+4,
m+4,

科目:初中數(shù)學 來源:不詳 題型:解答題
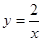 的圖像與一次函數(shù)
的圖像與一次函數(shù)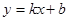 的圖像交于點A(m,2),點B(-2, n ),一次函數(shù)圖像與y軸的交點為C.求△AOC的面積。
的圖像交于點A(m,2),點B(-2, n ),一次函數(shù)圖像與y軸的交點為C.求△AOC的面積。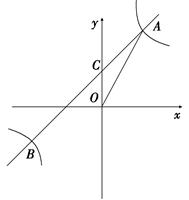
查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:單選題
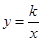 的圖象經過點(a,b),則它的圖象也一定經過( )
的圖象經過點(a,b),則它的圖象也一定經過( )| A.(-a,-b) | B.(a,-b) | C.(-a,b) | D.(0,0) |
查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:單選題
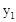 與反比例函數(shù)
與反比例函數(shù)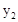 相交于點E(
相交于點E(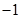 ,2),若
,2),若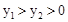 ,則
,則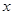 的取值范圍在數(shù)軸上表示正確的是【 】
的取值范圍在數(shù)軸上表示正確的是【 】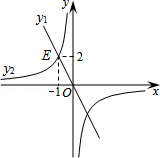
A.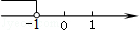 | B.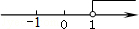 | C.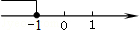 | D.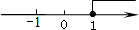 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com