【題目】計算： 
+2sin60°+|3﹣ 
|﹣（ 
﹣π）0 ．
【答案】解： 
+2sin60°+|3﹣ 
|﹣（ 
﹣π）0
=3+2× 
+3﹣ ﹣1
=3+ +3﹣ ﹣1
=5
【解析】本題涉及二次根式化簡、特殊角的三角函數值、絕對值、負整數指數冪4個考點．在計算時，需要針對每個考點分別進行計算，然后根據實數的運算法則求得計算結果．本題主要考查了實數的綜合運算能力，是各地中考題中常見的計算題型．解決此類題目的關鍵是熟練掌握二次根式化簡、特殊角的三角函數值、絕對值、負整數指數冪等考點的運算．
【考點精析】本題主要考查了零指數冪法則和特殊角的三角函數值的相關知識點，需要掌握零次冪和負整數指數冪的意義： a0=1（a≠0）;a-p=1/ap（a≠0，p為正整數）；分母口訣：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口訣：“123，321，三九二十七”才能正確解答此題．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知：E是∠AOB的平分線上一點，EC⊥OB，ED⊥OA，C、D是垂足，連接CD，且交OE于點F.
（1）求證：OE是CD的垂直平分線.
（2）若∠AOB=60，請你探究OE，EF之間有什么數量關系？并證明你的結論。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】從分別標有數﹣3，﹣2，﹣1，0，1，2，3的七張沒有明顯差別的卡片中，隨機抽取一張，所抽卡片上的數的絕對值不小于2的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某地區2014年投入教育經費2900萬元，2016年投入教育經費3509萬元．
（1）求2014年至2016年該地區投入教育經費的年平均增長率；
（2）按照義務教育法規定，教育經費的投入不低于國民生產總值的百分之四，結合該地區國民生產總值的增長情況，該地區到2018年需投入教育經費4250萬元，如果按（1）中教育經費投入的增長率，到2018年該地區投入的教育經費是否能達到4250萬元？請說明理由．
（參考數據： 
=1.1， 
=1.2， 
=1.3， 
=1.4）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上，張老師舉了下面的例題：
例1 等腰三角形
中，
，求
的度數.（答案：
）
例2 等腰三角形中，
，求的度數.（答案：
或
或
）
張老師啟發同學們進行變式，小敏編了如下一題：
變式 等腰三角形中，
，求的度數.
（1）請你解答以上的變式題.
（2）解（1）后，小敏發現，
的度數不同，得到的度數的個數也可能不同.如果在等腰三角形中，設
，當有三個不同的度數時，請你探索
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC的一邊AB上有一點P．
（1）能否在另外兩邊AC和BC上各找一點M、N，使得△PMN的周長最短．若能，請畫出點M、N的位置，若不能，請說明理由；
（2）若∠ACB=40°，在（1）的條件下，求出∠MPN的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB為⊙O的直徑，AC為⊙O的切線，OC交⊙O于點D，BD的延長線交AC于點E．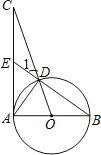
（1）求證：∠1=∠CAD；
（2）若AE=EC=2，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】荔枝是深圳的特色水果，小明的媽媽先購買了2千克桂味和3千克糯米糍，共花費90元；后又購買了1千克桂味和2千克糯米糍，共花費55元．（每次兩種荔枝的售價都不變）
（1）求桂味和糯米糍的售價分別是每千克多少元；
（2）如果還需購買兩種荔枝共12千克，要求糯米糍的數量不少于桂味數量的2倍，請設計一種購買方案，使所需總費用最低．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖①，已知：在△ABC中，∠BAC＝90°，AB=AC，直線m經過點A，BD⊥直線m, CE⊥直線m,垂足分別為點D、E.證明:DE=BD+CE.
（2）如圖②，將（1）中的條件改為：在△ABC中，AB=AC，D、A、E三點都在直線m上,并且有∠BDA=∠AEC=∠BAC=α,其中α為任意鈍角.請問結論DE=BD+CE是否成立?如成立,請你給出證明;若不成立,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com