求證：面積為S的矩形中任意三點（可以在矩形的邊界上）組成的三角形面積不超過 $數學公式$ S．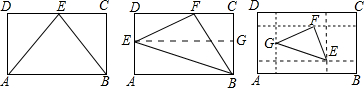

證明：分如下三種情況：
（1）如圖，這時△ABE的面積是矩形面積的一半；

（2）過E作AB的平行線，
∵S_△FEM= $\text{[math]}$ EM×CG，S_矩形DEGC=GC×EG，
顯然△EFM的面積小于矩形 $\text{[math]}$ DECG的面積，△BEM的面積小于矩形ABGE的面積，
所以△AEF的面積小于矩形 $\text{[math]}$ ABCD的面積；

（3）過E、F、G分別作如圖所示的AB、BC的平行線，
這四條線構成一個小矩形，由已經證明的（1）、（2）兩種情況可知，△EFG的面積不大于這個小矩形的面積的 $\text{[math]}$ ，
即△EFG的面積小于矩形ABCD的面積的 $\text{[math]}$ ；
綜上，面積為S的矩形中任意三點（可以在矩形的邊界上）組成的三角形面積不超過 $\text{[math]}$ S這一命題得證．
分析：利用三角形的面積求法與矩形的性質，比較面積大小，應分三種情況進行討論，①三角形一邊是矩形的一邊；②三個頂點在矩形上，三角形在矩形內部；③三個頂點都在矩形內部，利用圖形進行分析即可．
點評：此題主要考查了矩形的性質，利用三角形三個頂點位置不同進行分類討論是解決問題的關鍵．

練習冊系列答案

課課通課程標準思維方法與能力訓練系列答案

鐘書金牌教材金練系列答案

名牌學校分層課課練系列答案

培優奪冠王系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

求證：面積為S的矩形中任意三點（可以在矩形的邊界上）組成的三角形面積不超過

S．

查看答案和解析>>

科目：初中數學 來源： 題型：

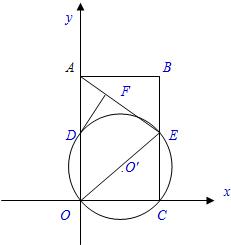19、如圖，在平面直角坐標系中，矩形ABCO的面積為15，且OA=OC+2，E為BC的中點，以OE為直徑的⊙O′交y軸于D點，過D作DF⊥AE于點F．
（1）求OA、OC的長；
（2）求證：DF為⊙O′的切線；
（3）小亮在解答本題時，發現△AOE是等腰三角形，且△AOE的面積是四邊形ABCO面積的一半．由此，他根據自己過去解題的實踐斷定：“直線BC上一定存在除點E以外的P點，使△AOP既是等腰三角形，又和△AOE的面積相等”．你同意他的斷言嗎？若同意，請你求出所有滿足上述條件的點P的坐標，若不同意，請你說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

在平面直角坐標系xOy中，矩形ABCO的面積為15，邊OA比OC大2，E為BC的中點，以OE為直徑的⊙O′交x軸于D點，過點D作DF⊥AE于F．
（1）求OA，OC的長；
（2）求證：DF為⊙O′的切線；
（3）由已知可得，△AOE是等腰三角形．那么在直線BC上是否存在除點E以外的點P，使△AOP也是等腰三角形？如果存在，請你證明點P與⊙O′的位置關系，如果不存在，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

（2013•武漢模擬）在面積為24的△ABC中，矩形DEFG的邊DE在AB上運動，點F、G分別在BC、AC上．
（1）若AE=8，DE=2EF，求GF的長；
（2）若∠ACB=90°，如圖2，線段DM、EN分別為△ADG和△BEF的角平分線，求證：MG=NF；
（3）請直接寫出矩形DEFG的面積的最大值．

查看答案和解析>>

同步練習冊答案

練習冊

高中

初中

小學

求證：面積為S的矩形中任意三點（可以在矩形的邊界上）組成的三角形面積不超過S．

求證：面積為S的矩形中任意三點（可以在矩形的邊界上）組成的三角形面積不超過 $數學公式$ S．