
【題目】如圖1,點P是菱形ABCD的對角線BD上的一動點,連接CP并延長交AD于E,交BA的延長線于點F.
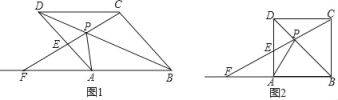
(1)求證:△APD≌△CPD;
(2)如圖2,當菱形ABCD變為正方形,且PC=2,tan∠PFA=![]() 時,求正方形ABCD的邊長.
時,求正方形ABCD的邊長.
【答案】(1)詳見解析;(2)![]()
【解析】
(1)根據菱形的性質得:AD=CD,∠ADP=∠CDP,根據SAS即可證明△APD≌△CPD;
(2)先根據tan∠PFA![]() ,設BC=a,則BF=2a,證明△DPC∽△BPF,得
,設BC=a,則BF=2a,證明△DPC∽△BPF,得![]() ,求FC=6,根據勾股定理列方程得:62=a2+(2a)2,可得正方形ABCD的邊長.
,求FC=6,根據勾股定理列方程得:62=a2+(2a)2,可得正方形ABCD的邊長.
(1)∵四邊形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.
在△APD和△CPD中,∵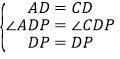 ,∴△APD≌△CPD(SAS);
,∴△APD≌△CPD(SAS);
(2)∵四邊形ABCD是正方形,∴∠ABC=90°,CD=BC.
∵tan∠PFA![]() ,設BC=a,則BF=2a.
,設BC=a,則BF=2a.
∵DC=BC=a,DC∥BF,∴∠DCP=∠PFB,∠CDP=∠PBF,∴△DPC∽△BPF,∴![]() .
.
∵PC=2,∴PF=4,∴FC=PC+PF=6.
在Rt△FCB中,FC2=BC2+FB2,∴62=a2+(2a)2,解得:a![]() 或
或![]() (舍),∴正方形ABCD的邊長為
(舍),∴正方形ABCD的邊長為![]() .
.


科目:初中數學 來源: 題型:
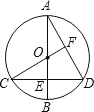
【題目】如圖,已知⊙O 的直徑 AB 垂直弦 CD 于點 E,連接 CO 并延長交 AD于點 F,且 CF⊥AD
(1)求證:點 E 是 OB 的中點;
(2)若 AB=12,求 CD 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() 中,
中,![]() ,
,![]() 于點
于點![]() ,
,![]() ,
,![]() .
.
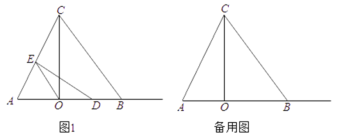
(1)求![]() ,
,![]() 的長
的長
(2)若點![]() 是射線
是射線![]() 上的一個動點,作
上的一個動點,作![]() 于點
于點![]() ,連結
,連結![]() .
.
①當點![]() 在線段
在線段![]() 上時,若
上時,若![]() 是以
是以![]() 為腰的等腰三角形,請求出所有符合條件的
為腰的等腰三角形,請求出所有符合條件的![]() 的長.
的長.
②設![]() 交直線
交直線![]() 于點
于點![]() ,連結
,連結![]() ,
,![]() ,若
,若![]() ,則
,則![]() 的長為______________.(直接寫出結果)
的長為______________.(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊![]() 中,
中,![]() 是邊
是邊![]() 上一點,連接
上一點,連接![]() ,將
,將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,則有以下四個結論:①
,則有以下四個結論:①![]() 是等邊三角形;②
是等邊三角形;②![]() ;③
;③![]() 的周長是10;④
的周長是10;④![]() .其中正確結論的序號是( )
.其中正確結論的序號是( )
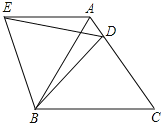
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
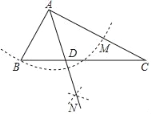
【題目】如圖,Rt△ABC中,∠BAC=90°,AB=6,sinC=![]() ,以點A為圓心,AB長為半徑作弧交AC于M,分別以B、M為圓心,以大于
,以點A為圓心,AB長為半徑作弧交AC于M,分別以B、M為圓心,以大于![]() BM長為半徑作弧,兩弧相交于點N,射線AN與BC相交于D,則AD的長為_____.
BM長為半徑作弧,兩弧相交于點N,射線AN與BC相交于D,則AD的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在圖(1)、(2)所示的△ABC中,AB=4,AC=6.將△ABC沿圖示中的虛線剪開裁剪辦法已在圖上標注,對于各圖中剪下的兩個陰影三角形而言,下列說法正確的是( )
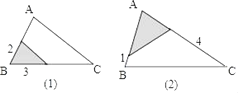
A. 只有(1)中的與△ABC相似 B. 只有(2)中的與△ABC相似
C. 都與△ABC相似 D. 都與△ABC不相似
查看答案和解析>>
科目:初中數學 來源: 題型:
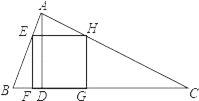
【題目】如圖,△ABC為銳角三角形,AD是BC邊上的高,正方形EFGH的一邊FG在BC上,頂點E,H分別在AB,AC上,已知BC=40cm,AD=30cm,求這個正方形的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是由8個大小相同的小正方體組合成的簡單幾何體.
(1)該幾何體的主視圖如圖所示,請在下面方格紙中分別畫出它的左視圖和俯視圖;(邊框線加粗畫出,并涂上陰影)
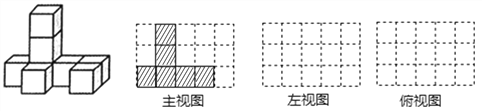
(2)如果在這個幾何體上再添加一些相同的小正方體,并保持這個幾何體的俯視圖和主視圖不變,那么請在下列網格圖中畫出添加小正方體后所得幾何體所有可能的左視圖.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com