
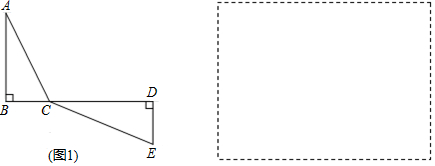
���� ��1������(j��)���ɶ���ֱ����ʽ��
��2������(j��)�����ε���߅�P(gu��n)ϵ�ɵã���(d��ng)�c(di��n)C��ֱ��AE�ϕr(sh��)��AC+CE��ֵ��С��
��3����(g��u)������ڈD1�ĈD3�����o��������(g��u)��ֱ�ǡ�AEF�����ù��ɶ������AE���L(zh��ng)��������(sh��)ʽ����Сֵ��
���  �⣺��1����CD=x��BD=12��
�⣺��1����CD=x��BD=12��
��BC=12-x��
�ɹ��ɶ����ã�AC+CE=$\sqrt{{3}^{2}+��12-x��^{2}}+\sqrt{{2}^{2}+{x}^{2}}$��
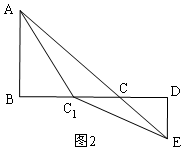
��2����(d��ng)�c(di��n)C��ֱ��AE�ϕr(sh��)����D2��AC+CE��ֵ��С��
�����ǣ�C1�Ǿ���BD������һ�c(di��n)��C1���cC�غϣ���
�ڡ�AC1E�У���AC1+EC1��AE��
��AC1+EC1��AC+CE��
��AC+CE��ֵ��С��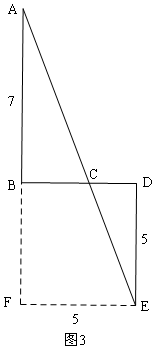
��3����D3������BD���քe�^�c(di��n)B��D��BD�ɂ�(c��)��AB��BD��ED��BD��
��֪AB=7��BD=DE=5���B�Y(ji��)AE��BD��C��
�ɣ�2���ã��˕r(sh��)AC+CE��ֵ��С��
�O(sh��)BC=x���tCD=5-x��
��AC+CE=$\sqrt{{x}^{2}+49}$+$\sqrt{��5-x��^{2}+25}$��
������(sh��)ʽ$\sqrt{{x}^{2}+49}$+$\sqrt{��5-x��^{2}+25}$����Сֵ���Ǿ���AE���L(zh��ng)��
�^E��EF��AB����AB�����L(zh��ng)����F��
���F=90�㣬
��AB��BD��ED��BD��
���FBD=��BDE=90�㣬
����߅��EFBD�Ǿ��Σ�
��EF=BD=5��BF=DE=5��
��AF=5+7=12��
��Rt��AEF�У��t���ɶ����ã�AE=$\sqrt{1{2}^{2}+{5}^{2}}$=13��
�����(sh��)ʽ$\sqrt{{x}^{2}+49}$+$\sqrt{��5-x��^{2}+25}$����Сֵ��13��
�c(di��n)�u(p��ng) ���}���������·�����}�����_�_��C�c(di��n)��λ���ǽ��}���P(gu��n)�I�����}߀�����˃��c(di��n)֮�g������̻������ε���߅�P(gu��n)ϵ�����ɶ�����



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
 ��D��ʾ�������������_�Ă�(g��)��(sh��)�У�������
��D��ʾ�������������_�Ă�(g��)��(sh��)�У�������| A�� | 0��(g��) | B�� | 1��(g��) | C�� | 2��(g��) | D�� | 3��(g��) |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
| A�� | -3 | B�� | -2 | C�� | 0 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
| A�� | 1 | B�� | 5 | C�� | -1 | D�� | -5 |
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com