
【題目】如圖,將兩塊直角三角尺的直角頂點C疊放在一起.
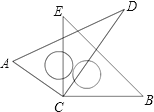
(1)判斷∠ACE與∠BCD的大小關系,并說明理由;
(2)若∠DCE=30°,求∠ACB的度數;
(3)猜想:∠ACB與∠DCE有怎樣的數量關系,并說明理由.
【答案】(1)∠ACE=∠BCD;(2)150°;(3)∠ACB+∠DCE=180°,見解析
【解析】
試題分析:(1)根據余角的性質,可得答案;
(2)根據余角的定義,可得∠ACE,根據角的和差,可得答案;
(3)根據補角的定義,可得答案.
解:(1)∠ACE=∠BCD,理由如下:
∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
∴∠ACE=∠BCD;
(2)由余角的定義,得∠ACE=90°﹣∠DCE=90°﹣30°=60°,
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°;
(3)∠ACB+∠DCE=180°,理由如下:
由角的和差,得∠ACB=∠BCE+∠ACE,
∠ACB+∠DCE=∠BCE+(∠ACE+DCE)=∠BCE+∠ACE=180°.


科目:初中數學 來源: 題型:
【題目】觀察一組數據:2,4,7,11,16,22,29,…,它們有一定的規律,若記第一個數為a1,第二個數記為a2,…,第n個數記為an.
(1)請寫出29后面的第一個數;
(2)通過計算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根據你發現的規律求a100的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義![]() 為一次函數
為一次函數![]() 的特征數.
的特征數.
(1)若特征數是![]() 的一次函數為正比例函數,求
的一次函數為正比例函數,求![]() 的值;
的值;
(2)設點![]() 分別為拋物線y=(3x+2m)(x-4)
分別為拋物線y=(3x+2m)(x-4)![]() 與
與![]() 軸的交點,其中
軸的交點,其中![]() ,且
,且![]() 的面積為4,
的面積為4,![]() 為原點,求圖象過
為原點,求圖象過![]() 兩點的一次函數的特征數.
兩點的一次函數的特征數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=90°, D是AB邊上一點,且DB=DC,過BC上一點P(不包括B,C二點)作PE⊥AB,垂足為點E, PF⊥CD,垂足為點F,已知AD:DB=1:4,BC=![]() ,求PE+PF的長.
,求PE+PF的長.
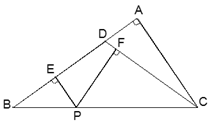
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, A、B兩地被池塘隔開, 小明通過下列方法測出了A、B間的距離: 先在AB外選一點C, 然后測出AC、BC的中點M、N,并測量出MN的長為12m, 由此他就知道了A、B間的距離.有關他這次探究活動的描述錯誤的是( )
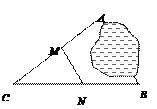
A. CM : MA = 1 : 2 B. MN∥AB C. △CMN ∽△CAB D. AB=24m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有以下運算程序,如圖所示:
![]()
比如,輸入數對(2,1),輸出W=2.
(1)若輸入數對(1,﹣2),則輸出W= ;
(2)分別輸入數對(m,﹣n)和(﹣n,m),輸出的結果分別是W1,W2,試比較W1,W2的大小,并說明理由;
(3)設a=|x﹣2|,b=|x﹣3|,若輸入數對(a,b)之后,輸出W=26,求a+b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com