
【題目】如圖,拋物線L:![]() 與x軸交于A、B(3,0)兩點(A在B的左側),與y軸交于點C(0,3),已知對稱軸x=1.
與x軸交于A、B(3,0)兩點(A在B的左側),與y軸交于點C(0,3),已知對稱軸x=1.
(1)求拋物線L的解析式;
(2)將拋物線L向下平移h個單位長度,使平移后所得拋物線的頂點落在△OBC內(包括△OBC的邊界),求h的取值范圍;
(3)設點P是拋物線L上任一點,點Q在直線l:x=﹣3上,△PBQ能否成為以點P為直角頂點的等腰直角三角形?若能,求出符合條件的點P的坐標;若不能,請說明理由.

【答案】(1)![]() ;(2)2≤h≤4;(3)P(1,4)或(0,3)或(
;(2)2≤h≤4;(3)P(1,4)或(0,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
試題分析:(1)利用待定系數法求出拋物線的解析式即可;
(2)先求出直線BC解析式為y=﹣x+3,再求出拋物線頂點坐標,得出當x=1時,y=2;結合拋物線頂點坐即可得出結果;
(3)設P(m,![]() ),Q(﹣3,n),(3)設P(m,
),Q(﹣3,n),(3)設P(m,![]() ),Q(﹣3,n).分兩種情況討論:①當P點在x軸上方時,過P點作PM垂直于y軸,交y軸與M點,過B點作BN垂直于MP的延長線于N點,可證明△PQM≌△BPN(AAS),得到PM=BN,由PM=BN=
),Q(﹣3,n).分兩種情況討論:①當P點在x軸上方時,過P點作PM垂直于y軸,交y軸與M點,過B點作BN垂直于MP的延長線于N點,可證明△PQM≌△BPN(AAS),得到PM=BN,由PM=BN=![]() ,根據B點坐標可得PN=3﹣m,且PM+PN=6,得到
,根據B點坐標可得PN=3﹣m,且PM+PN=6,得到![]() ,解方程即可.
,解方程即可.
②當P點在x軸下方時,過P點作PM垂直于l于M點,過B點作BN垂直于MP的延長線與N點,同理可得△PQM≌△BPN,得到PM=BN, PM=6﹣(3﹣m)=3+m,BN=![]() ,則
,則![]() ,解方程即可.
,解方程即可.
試題解析:(1)∵拋物線的對稱軸x=1,B(3,0),∴A(﹣1,0).
∵拋物線![]() 過點C(0,3),∴當x=0時,c=3.
過點C(0,3),∴當x=0時,c=3.
又∵拋物線![]() 過點A(﹣1,0),B(3,0),∴
過點A(﹣1,0),B(3,0),∴![]() ,∴
,∴![]() ,∴拋物線的解析式為:
,∴拋物線的解析式為:![]() ;
;
(2)∵C(0,3),B(3,0),∴直線BC解析式為y=﹣x+3,∵![]() =
=![]() ,∴頂點坐標為(1,4)
,∴頂點坐標為(1,4)
∵對于直線BC:y=﹣x+1,當x=1時,y=2;將拋物線L向下平移h個單位長度,∴當h=2時,拋物線頂點落在BC上;
當h=4時,拋物線頂點落在OB上,∴將拋物線L向下平移h個單位長度,使平移后所得拋物線的頂點落在△OBC內(包括△OBC的邊界),則2≤h≤4;
(3)設P(m,![]() ),Q(﹣3,n).分兩種情況討論:
),Q(﹣3,n).分兩種情況討論:
①當P點在x軸上方時,過P點作PM垂直于y軸,交y軸與M點,過B點作BN垂直于MP的延長線于N點,如圖所示,∵B(3,0),∵△PBQ是以點P為直角頂點的等腰直角三角形,∴∠BPQ=90°,BP=PQ,則∠PMQ=∠BNP=90°,∠MPQ=∠NBP,在△PQM和△BPN中,∵∠PMQ=∠BNP,∠MPQ=∠BNP,PQ=BP,∴△PQM≌△BPN(AAS),∴PM=BN,∵PM=BN=![]() ,根據B點坐標可得PN=3﹣m,且PM+PN=6,∴
,根據B點坐標可得PN=3﹣m,且PM+PN=6,∴![]() ,解得:m=1或m=0,∴P(1,4)或P(0,3).
,解得:m=1或m=0,∴P(1,4)或P(0,3).
②當P點在x軸下方時,過P點作PM垂直于l于M點,過B點作BN垂直于MP的延長線與N點,同理可得△PQM≌△BPN,∴PM=BN,∴PM=6﹣(3﹣m)=3+m,BN=![]() ,則
,則![]() ,解得m=
,解得m=![]() 或
或![]() ,∴P(
,∴P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
綜上可得,符合條件的點P的坐標是(1,4),(0,3),(![]() ,
,![]() )和(
)和(![]() ,
,![]() ).
).
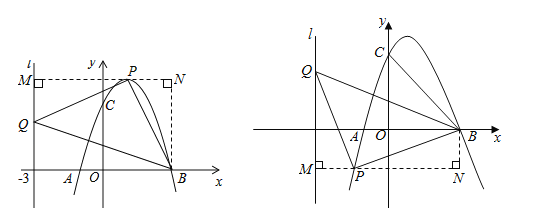


科目:初中數學 來源: 題型:
【題目】 (2016柳州)如圖1,拋物線![]() 的頂點坐標為(0,﹣1),且經過點A(﹣2,0).
的頂點坐標為(0,﹣1),且經過點A(﹣2,0).

(1)求拋物線的解析式;
(2)若將拋物線![]() 中在x軸下方的圖象沿x軸翻折到x軸上方,x軸上方的圖象保持不變,就得到了函數
中在x軸下方的圖象沿x軸翻折到x軸上方,x軸上方的圖象保持不變,就得到了函數![]() 圖象上的任意一點,直線l是經過(0,1)且平行與x軸的直線,過點P作直線l的垂線,垂足為D,猜想并探究:PO與PD的差是否為定值?如果是,請求出此定值;如果不是,請說明理由.
圖象上的任意一點,直線l是經過(0,1)且平行與x軸的直線,過點P作直線l的垂線,垂足為D,猜想并探究:PO與PD的差是否為定值?如果是,請求出此定值;如果不是,請說明理由.
(注:在解題過程中,如果你覺得有困難,可以閱讀下面的材料)
附閱讀材料:
1.在平面直角坐標系中,若A、B兩點的坐標分別為A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),則A,B兩點間的距離為|AB|=
),則A,B兩點間的距離為|AB|=![]() ,這個公式叫兩點間距離公式.
,這個公式叫兩點間距離公式.
例如:已知A,B兩點的坐標分別為(﹣1,2),(2,﹣2),則A,B兩點間的距離為|AB|=![]() =5.
=5.
2.因式分解:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=12cm,BC=6cm,點P沿AB邊從點A開始向點B以2cm/秒的速度移動;點Q沿DA邊從點D開始向點A以1cm/秒的速度移動,如果P、Q同時出發,用t(秒)表示移動的時間(0<t<6). 
(1)當t為何值時,△PBC為等腰直角三角形?
(2)求當移動到△QAP為等腰直角三角形時斜邊QP的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com