【題目】過線段
的兩端作
于
，
于
，連
、
交于
，
，
，那么點到線段的距離為________．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖,拋物線y=x2-3與直線y=kx(k≠0)相交于點A和點B,則一元二次方程x2-kx-3=0的解的情況是（ ）
A. 有兩個不相等的正實根 B. 有兩個不相等的負實根
C. 一個正實根、一個負實根 D. 有兩個相等的實數根
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用兩個全等的等邊
和
拼成如圖的菱形
．現把一個含
角的三角板與這個菱形疊合，使三角板的角的頂點與點
重合，兩邊分別與
、
重合．將三角板繞點逆時針方向旋轉．
如圖，當三角板的兩邊分別與菱形的兩邊
、
相交于點
、
時，探求
、
、
的數量關系，并說明理由；
繼續旋轉三角板，當兩邊
、
分別交、
的延長線于點、時，畫出旋轉后相應的圖形，并直接寫出、、滿足的數量關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在平行四邊形ABCD中，E、F分別為邊AB、CD的中點，BD是對角線，AG∥DB交CB的延長線于G．
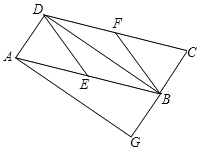
（1）求證：△ADE≌△CBF；
（2）若四邊形 BEDF是菱形，則四邊形AGBD是什么特殊四邊形？并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在四邊形ABCD中，
，
，
．
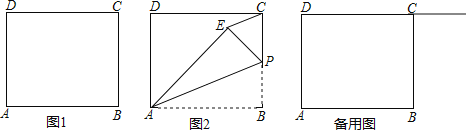
為邊BC上一點，將
沿直線AP翻折至
的位置
點B落在點E處
如圖1，當點E落在CD邊上時，利用尺規作圖，在圖1中作出滿足條件的圖形不寫作法，保留作圖痕跡，用2B鉛筆加粗加黑
并直接寫出此時
______；
如圖2，若點P為BC邊的中點，連接CE，則CE與AP有何位置關系？請說明理由；
點Q為射線DC上的一個動點，將
沿AQ翻折，點D恰好落在直線BQ上的點
處，則
______；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是等邊三角形ABC內一點，且PA=3，PB=4，PC=5，若將△APB繞著點B逆時針旋轉后得到△CQB。
（1）△BPQ是 三角形；
（2）求PQ的長度；
（3）求∠APB的度數。
查看答案和解析>>
科目：初中數學 來源： 題型：
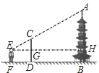
【題目】如圖，小明欲測量一座古塔的高度，他拿出一根竹桿豎直插在地面上，然后自己退后，使眼睛通過竹桿的頂端剛好看到塔頂，若小明眼睛離地面
，竹桿頂端離地面
，小明到竹桿的距離
，竹桿到塔底的距離
，求這座古塔的高度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）操作與探究：如圖，矩形紙片ABCD中，AB=8，將紙片折疊，使頂點B落在邊AD的E點上，折痕的一端G點在邊BC上，BG=10．
①第一次折疊：當折痕的另一端點F在AB邊上時，如圖1，求折痕GF的長；
②第二次折疊：當折痕的另一端點F在AD邊上時，如圖2，證明四邊形BGEF為菱形，并求出折痕GF的長．
（2）拓展延伸：通過操作探究發現在矩形紙片ABCD中，AB=5，AD=13．如圖3所示，折疊紙片，使點A落在BC邊上的A′處，折痕為PQ．當點A′在BC邊上移動時，折痕的端點P，Q也隨之移動．若限定點P，Q分別在AB，AD邊上移動，則點A′在BC邊上可移動的最大距離是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
