
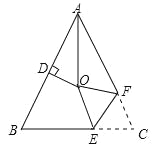
【題目】如圖,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,則∠CFE為________度.
【答案】50°
【解析】
連接OB,OC,先求出∠BAO=25°,進而求出∠OBC=40°,求出∠COE=∠OCB=40°,最后根據等腰三角形的性質,問題即可解決.
解:如圖,連接OB,
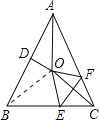
∵∠BAC=50°,AO為∠BAC的平分線,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×50°=25°.
×50°=25°.
又∵AB=AC,
∴∠ABC=∠ACB=65°.
∵DO是AB的垂直平分線,
∴OA=OB,
∴∠ABO=∠BAO=25°,
∴∠OBC=∠ABC-∠ABO=65°-25°=40°.
∵AO為∠BAC的平分線,AB=AC,
∴直線AO垂直平分BC,
∴OB=OC,
∴∠OCB=∠OBC=40°,
∵將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,
∴OE=CE.
∴∠COE=∠OCB=40°;
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-40°-40°=100°,
∴∠CEF=![]() ∠CEO=50°.
∠CEO=50°.
故答案為:50°.


科目:初中數學 來源: 題型:
【題目】某文具店到批發市場選購A、B兩種文具,批發價分別為14元/個、10元/個.若該店零售A、B兩種文具的每天銷量y(個)與零售價x(元/個)都是一次函數y=kx+20的關系,如圖所示. 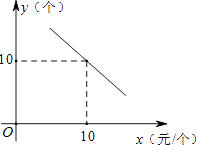
(1)求此一次函數的關系式;
(2)現批發市場進行促銷活動,憑會員卡(240元/張)在該批發市場購買所有物品均進行打折優惠,若文具店購買A、B兩種文具各50個,問打折小于多少折時,采用購買會員卡的方式合算;
(3)在文具店不購買會員卡的情況下,若A種文具零售價比B種文具零售價高2元/個,求這兩種文具每天的銷售總利潤W(元)與A種文具零售價x(元/個)之間的函數關系式,并說明當A種文具的零售價為多少時,每天的銷售利潤最大. (說明:本題不要求寫出自變量x的取值范圍)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大酒店有108個相同規格的房間需要裝飾.一天,3名師傅去裝飾8個房間,結果其中有40平方米未來得及裝飾;同樣一天5名徒弟去恰好裝飾完9個房間.已知每名師傅比徒弟一天多裝飾30平方米.
(1)求每個房間需要裝飾的面積;
(2)每名師傅每天裝飾多少平方米?每名徒弟呢?
(3)若由1名師傅帶2名徒弟去裝飾這108個房間,需要幾天才能完成?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB、AC的垂直平分線分別交BC于點E、F.
(1)若△AEF的周長為10cm,則BC的長為______cm.
(2)若∠EAF=100°,則∠BAC______.
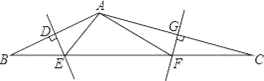
查看答案和解析>>
科目:初中數學 來源: 題型:
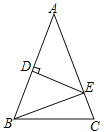
【題目】(3分)如圖,△ABC中,AB=AC,AB的垂直平分線交邊AB于D點,交邊AC于E點,若△ABC與△EBC的周長分別是40cm,24cm,則AB= cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,網格圖中小方格都是邊長為1個單位長度的小正方形,已知三角形ABC的三個頂點都在網格的格點上,按要求完成下列各小題.
(1)請在圖中畫出將三角形ABC先向上平移1個單位長度,再向右平移3個單位長度后的圖形,即三角形A′B′C′,并指出圖中相等的線段;
(2)在(1)的基礎上,A′B′,B′C′分別與AC交于點E,F.若∠A=50°,∠C′=51°,分別求出∠A′EF與∠B′FC的度數.
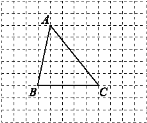
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P為⊙O外一點,PA、PB為⊙O的切線,A、B為切點,AC為⊙O的直徑,PO交于⊙O于點E. 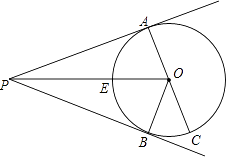
(1)試判斷∠APB與∠BAC的數量關系;
(2)若⊙O的半徑為4,P是⊙O外一動點,是否存在點P,使四邊形PAOB為正方形?若存在,請求出PO的長,并判斷點P的個數及其滿足的條件;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】手機上網已經成為當今年輕人時尚的網絡生活,某網絡公司看中了這種商機,推出了兩種手機上網的計費方式:方式A以每分鐘0.1元的價格按上網時間計費;方式B除收月基費20元外,再以每分鐘0.06元的價格按上網時間計費.假設某客戶月手機上網的時間為x分鐘,上網費用為y元. 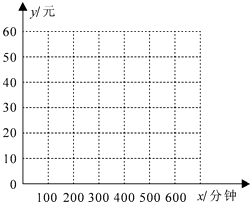
(1)分別寫出該客戶按A、B兩種方式的上網費y(元)與每月上網時間x(分鐘)的函數關系式,并在右圖的坐標系中畫出這兩個函數的圖象;
(2)如何選擇計費方式能使該客戶上網費用更合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com