
【題目】如圖,在正方形ABCD中,AD=4,E,F分別是CD,BC上的一點,且∠EAF=45°,EC=1,將△ADE繞點A沿順時針方向旋轉90°后與△ABG重合,連接EF,過點B作BM∥AG,交AF于點M,則以下結論:①DE+BF=EF②BF=![]() ; ③AF=
; ③AF=![]() ;④
;④![]() 中正確的是( )
中正確的是( )
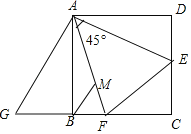
A. ①③④B. ②③④C. ①②③D. ①②④
科目:初中數學 來源: 題型:
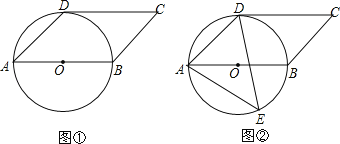
【題目】已知四邊形ABCD是平行四邊形,以AB為直徑的⊙O經過點D,∠DAB=45°.
(1)如圖①,判斷CD與⊙O的位置關系,并說明理由;
(2)如圖②,E是⊙O上一點,且點E在AB的下方,若⊙O的半徑為3cm,AE=5cm,求點E到AB的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知m,n分別是關于x的一元二次方程ax2+bx+c=a與ax2+bx+c=b的一個根,且m=n+1.
(1)當m=2,a=﹣1時,求b與c的值;
(2)用只含字母a,n的代數式表示b;
(3)當a<0時,函數y=ax2+bx+c滿足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,在△ABC中,AB=AC,在射線AB上截取線段BD,在射線CA上截取線段CE,連結DE,DE所在直線交直線BC于點M.
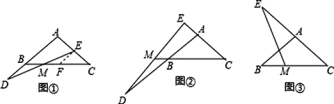
猜想:當點D在邊AB的延長線上,點E在邊AC上時,過點E作EF∥AB交BC于點F,如圖①.若BD=CE,則線段DM、EM的大小關系為 .
探究:當點D在邊AB的延長線上,點E在邊CA的延長線上時,如圖②.若BD=CE,判斷線段DM、EM的大小關系,并加以證明.
拓展:當點D在邊AB上(點D不與A、B重合),點E在邊CA的延長線上時,如圖③.若BD=1,CE=4,DM=0.7,求EM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,以BC為直徑的⊙O中,點A、E為圓周上兩點,過點A作AD⊥BC,垂足為D,作AF⊥CE的延長線于點F,垂足為F,連接AC、AO,已知BD=EF,BC=4.
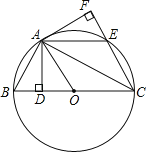
(1)求證:∠ACB=∠ACF;
(2)當∠AEF= °時,四邊形AOCE是菱形;
(3)當AC= 時,四邊形AOCE是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有七張正面分別標有數字﹣3,﹣2,﹣1,0,1,2,3的卡片,它們除數字不同外其余全部相同.現將它們背面朝上,洗勻后從中隨機抽取一張,記卡片上的數字為a,則使關于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有兩個不相等的實數根,且以x為自變量的二次函數y=x2﹣(a2+1)x﹣a+2的圖象不經過點(1,0)的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com