
【題目】兩個三角板![]() ,
,![]() ,按如圖所示的位置擺放,點
,按如圖所示的位置擺放,點![]() 與點
與點![]() 重合,邊
重合,邊![]() 與邊
與邊![]() 在同一條直線上(假設圖形中所有的點,線都在同一平面內).其中,
在同一條直線上(假設圖形中所有的點,線都在同一平面內).其中,![]() ,
,![]() ,
,![]() .現固定三角板
.現固定三角板![]() ,將三角板
,將三角板![]() 沿射線
沿射線![]() 方向平移,當點
方向平移,當點![]() 落在邊
落在邊![]() 上時停止運動.設三角板平移的距離為
上時停止運動.設三角板平移的距離為![]() ,兩個三角板重疊部分的面積為
,兩個三角板重疊部分的面積為![]() .
.

(1)當點![]() 落在邊
落在邊![]() 上時,
上時,![]() ;
;
(2)求![]() 關于
關于![]() 的函數解析式,并寫出自變量
的函數解析式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)設邊![]() 的中點為點
的中點為點![]() ,邊
,邊![]() 的中點為點
的中點為點![]() .直接寫出在三角板平移過程中,點
.直接寫出在三角板平移過程中,點![]() 與點
與點![]() 之間距離的最小值.
之間距離的最小值.
【答案】(1)![]() ;(2)
;(2)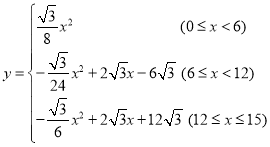 ;(3)
;(3)![]() .
.
【解析】
試題分析:
(1)由銳角三角函數,得到![]() 的長,進而可得
的長,進而可得![]() 的長,由矩形的性質,可得答案;
的長,由矩形的性質,可得答案;
(2)分類討論:①當![]() 時,根據三角形的面積公式,可得答案;②當
時,根據三角形的面積公式,可得答案;②當![]() 時,
時,
③當![]() 時,根據面積的和差,可得答案;
時,根據面積的和差,可得答案;
(3)根據點與直線上所有點的連線中垂線段最短,可得![]() 在線段
在線段![]() 上,根據三角形的
上,根據三角形的
中位線,可得![]() 的長,根據銳角三角函數,可得
的長,根據銳角三角函數,可得![]() 的長,根據線段的和差,可得答案.
的長,根據線段的和差,可得答案.
試題解析:
解:(1)如圖1所示:作![]() 于
于![]() 點.
點.
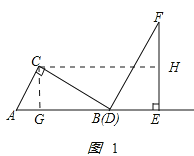
在![]() 中,由
中,由![]() ,
,![]() ,得:
,得:![]() =
=![]() .
.
在![]() 中,
中,![]() .四邊形
.四邊形![]() 是矩形,
是矩形,![]() ,故答案為:
,故答案為:![]() ;
;
(2)①當![]() 時,如圖2所示.
時,如圖2所示.
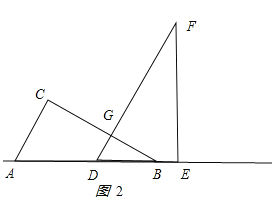
![]() ,
,![]() ,
,![]() ,得:
,得:![]() ,
, ![]() ,
,
重疊部分的面積為![]() ;
;
②當![]() 時,如圖3所示.
時,如圖3所示.
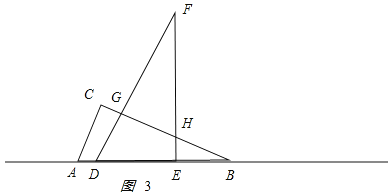
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
重疊部分的面積為![]() ,
,
即![]() ,
,
化簡,得![]() ;
;
③當![]() 時,如圖4所示.
時,如圖4所示.
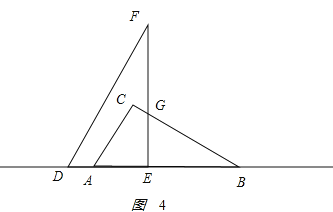
![]() ,
, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
重疊部分的面積為![]() ,
,
即![]() ,
,
化簡,得![]() ;
;
綜上所述: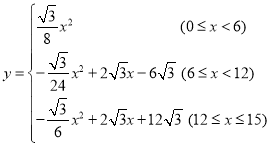 ;
;
(3)如圖5所示作![]() 于
于![]() 點.
點.
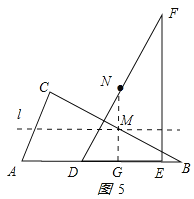
點![]() 在
在![]() 上時
上時![]() 最短,
最短,![]() 是
是![]() ,
,![]() .
. ![]() ,
,![]() ,
,![]() ,
,![]()


科目:初中數學 來源: 題型:
【題目】利用反證法證明命題“四邊形中至少有一個角是鈍角或直角”時,應假設( )
A. 四邊形中至多有一個內角是鈍角或直角
B. 四邊形中所有內角都是銳角
C. 四邊形的每一個內角都是鈍角或直角
D. 四邊形中所有內角都是直角
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】孔明是一個喜歡探究鉆研的同學,他在和同學們一起研究某條拋物線![]() 的性質時,將一把直角三角板的直角頂點置于平面直角坐標系的原點
的性質時,將一把直角三角板的直角頂點置于平面直角坐標系的原點![]() ,兩直角邊與該拋物線交于
,兩直角邊與該拋物線交于![]() 、
、![]() 兩點,請解答以下問題:
兩點,請解答以下問題:
(1)若測得![]() (如圖1),求
(如圖1),求![]() 的值;
的值;
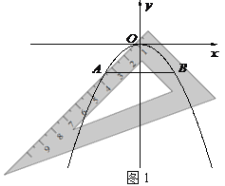
(2)對同一條拋物線,孔明將三角板繞點![]() 旋轉到如圖2所示位置時,過
旋轉到如圖2所示位置時,過![]() 作
作![]() 軸于點
軸于點![]() ,測得
,測得![]() ,寫出此時點
,寫出此時點![]() 的坐標,并求點
的坐標,并求點![]() 的橫坐標;
的橫坐標;
(3)對該拋物線,孔明將三角板繞點![]() 旋轉任意角度時驚奇地發現,交點
旋轉任意角度時驚奇地發現,交點![]() 、
、![]() 的連線段總經過一個固定的點,試說明理由并求出該點的坐標.
的連線段總經過一個固定的點,試說明理由并求出該點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小美周末來到公園,發現在公園一角有一種“守株待兔”游戲。游戲設計者提供了一只兔子和一個有A、B、C、D、E五個出入口的兔籠,而且籠內的兔子從每個出入口走出兔籠的機會是均等的。規定:①玩家只能將小兔從A、B兩個出入口放入;
②如果小兔進入籠子后選擇從開始進入的出入口離開,則可獲得一只價值5元小兔玩具,否則應付費3元。
(1)、問小美得到小兔玩具的機會有多大?
(2)、假設有100人次玩此游戲,估計游戲設計者可賺多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.若a、b、c是△ABC的三邊,則a2b2c2;
B.若a、b、c是Rt△ABC的三邊,則a2b2c2;
C.若a、b、c是Rt△ABC的三邊,∠A=90°,則a2b2c2;
D.若a、b、c是Rt△ABC的三邊,∠C=90°,則a2b2c2;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若函數y=(k﹣1)x|k|+b+1是正比例函數,則k和b的值為( )
A.k=±1,b=﹣1
B.k=±1,b=0
C.k=1,b=﹣1
D.k=﹣1,b=﹣1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com