
【題目】如圖,直線y=![]() x與反比例函數的圖象交于點A(3,a),第一象限內的點B在這個反比例函數圖象上,OB與x軸正半軸的夾角為α,且tanα=
x與反比例函數的圖象交于點A(3,a),第一象限內的點B在這個反比例函數圖象上,OB與x軸正半軸的夾角為α,且tanα=![]() .
.
(1)求反比例函數的解析式;
(2)求點B的坐標;
(3)求S△OAB.
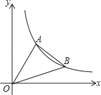
【答案】(1) y=![]() ; (2) B的坐標為(6,2);(3)9.
; (2) B的坐標為(6,2);(3)9.
【解析】分析:(1)由點A在直線上,將x=3代入帶直線解析式中求出a值,再由點A的坐標利用反比例函數圖象上點的坐標特征即可得出k值,由此即可得出結論;
(2)設點B坐標為(x, ![]() ),利用正切的定義結合tanα=
),利用正切的定義結合tanα=![]() ,即可得出關于x的分式方程,解方程即可得出x的值,由此即可得出點B的坐標;
,即可得出關于x的分式方程,解方程即可得出x的值,由此即可得出點B的坐標;
(3)設直線OB為y=kx,由點B的坐標利用待定系數法即可求出直線OB的解析式,過A點做AC⊥x軸,交OB于點C,利用分割法結合三角形的面積公式即可得出結論.
詳解:
(1)∵直線y=![]() x與反比例函數的圖象交于點A(3,a),
x與反比例函數的圖象交于點A(3,a),
∴a=![]() ×3=4,
×3=4,
∴點A的坐標為(3,4),
∴k=3×4=12,
∴反比例函數解析式y=![]() .
.
(2)∵點B在這個反比例函數圖象上,設點B坐標為(x, ![]() ),
),
∵tanα=![]() ,
,
∴![]() =
=![]() ,解得:x=±6,
,解得:x=±6,
∵點B在第一象限,
∴x=6,
∴點B的坐標為(6,2).
(3)設直線OB為y=kx,(k≠0),將點B(6,2)代入得:2=6k,
解得:k=![]() ,
,
∴OB直線解析式為:y=![]() x.
x.
過A點做AC⊥x軸,交OB于點C,如圖所示:
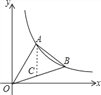
則點C坐標為(3,1),
∴AC=3.
S△OAB的面積=S△OAC的面積+S△ACB的面積=![]() ×|AC|×6=9.
×|AC|×6=9.
∴△OAB的面積為9.


科目:初中數學 來源: 題型:
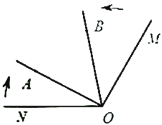
【題目】如圖,已知![]() ,射線
,射線![]() 從
從![]() 的位置開始繞點
的位置開始繞點![]() 按順時針方向旋轉,速度是每秒
按順時針方向旋轉,速度是每秒![]() ,同時射線
,同時射線![]() 從
從![]() 的位置開始繞點
的位置開始繞點![]() 按逆時針方向旋轉,速度是每秒
按逆時針方向旋轉,速度是每秒![]() ,設旋轉時間為
,設旋轉時間為![]() 秒
秒![]() .
.
(1)用含![]() 的代數式表示
的代數式表示![]() 和
和![]() 的度數;
的度數;
(2)在旋轉過程中,當![]() 等于
等于![]() 時,求
時,求![]() 的值;
的值;
(3)在旋轉過程中是否存在這樣的![]() ,使得射線
,使得射線![]() 恰好是圖中某個角的平分線?如果存在,請求出
恰好是圖中某個角的平分線?如果存在,請求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
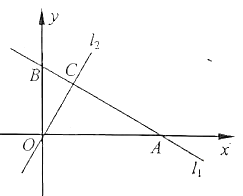
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖象
的圖象![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于
軸交于![]() 兩點,正比例函數的圖象
兩點,正比例函數的圖象![]() 與
與![]() 交于點
交于點![]() .
.
(1)求點![]() 坐標;
坐標;
(2)求![]() 的表達式;
的表達式;
(3)求![]() 和
和![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
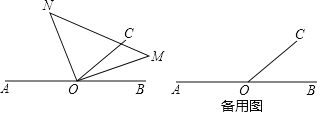
【題目】如圖,已知O是直線AB上一點,∠BOC<90°,三角板(MON)的直角頂點落在點O處現將三角板繞著點O旋轉,并保持OM和OC在直線AB的同一側.
(1)若∠BOC=50°
①當OM平分∠BOC時,求∠AON的度數.
②當OM在∠BOC內部,且∠AON=3∠COM時,求∠CON的度數:
(2)當∠COM=2∠AON時,請畫出示意圖,猜想∠AOM與∠BOC的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究:
如圖,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,其中
兩點,其中![]() .
.

(1)求![]() 的值;
的值;
(2)若點![]() 是直線
是直線![]() 上的一個動點,當點
上的一個動點,當點![]() 僅在第一象限內運動時,試寫出
僅在第一象限內運動時,試寫出![]() 的面積
的面積![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)探索:
①在(2)條件下,當點![]() 運動到什么位置時,
運動到什么位置時,![]() 的面積是
的面積是![]() ;
;
②在①成立的情況下,在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使△
,使△![]() 是等腰三角形?若存在,請寫出滿足條件的所有
是等腰三角形?若存在,請寫出滿足條件的所有![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售甲、乙兩種商品,現有如下信息:
請結合以上信息,解答下列問題:
(1)求甲、乙兩種商品的進貨單價;
(2)已知甲、乙兩種商品的零售單價分別為2元、3元,該商店平均每天賣出甲商品500件和乙商品1300件,經市場調查發現,甲種商品零售單價每降0.1元,甲種商品每天可多銷售100件,商店決定把甲種商品的零售單價下降m(m>0)元,在不考慮其他因素的條件下,求當m為何值時,商店每天銷售甲、乙兩種商品獲取的總利潤為1800元(注:單件利潤=零售單價﹣進貨單價)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年上半年撫州市各級各類中小學(含中等職業學校)開展了“萬師訪萬家”活動.某縣家訪方式有:A.上門走訪;B.電話訪問;C.網絡訪問(班級微信或QQ群);D.其他.該縣教育局負責人從“萬師訪萬家”平臺上隨機抽取本縣一部分老師的家訪情況,繪制了如圖所示兩幅尚不完整的統計圖.
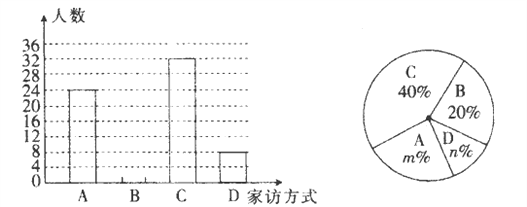
根據圖中提供的信息,解答下列問題:
(1)這次被抽查的家訪老師共有多少人?扇形統計圖中,“A”所對應的圓心角的度數為多少?
(2)請補全條形統計圖.
(3)已知該縣共有3500位老師參與了這次“萬師訪萬家”活動,請估計該縣共有多少位老師采用的是上門走訪的方式進行家訪的?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,用三個同(1)圖的長方形和兩個同(2)圖的長方形用兩種方式去覆蓋一個大的長方形![]() ,兩種方式為覆蓋的部分(陰影部分)的周長一樣,那么(1)圖中長方形的面積
,兩種方式為覆蓋的部分(陰影部分)的周長一樣,那么(1)圖中長方形的面積![]() 與(2)圖長方形的面積
與(2)圖長方形的面積![]() 的比是( )
的比是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com