Question

【題目】已知點 C為線段 AB上一點，分別以 AC、BC為邊在線段 AB同側作△ACD和△BCE，且 CA＝CD，CB＝CE，∠ACD＝∠BCE，直線 AE與 BD交于點 F

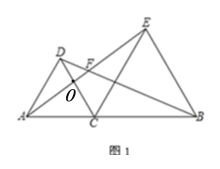
(1)如圖 1，若∠ACD＝60°，則∠AFD＝

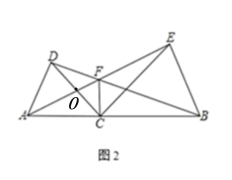
(2)如圖 2，若∠ACD＝α，則∠AFB＝ （用含α的式子表示），并說明理由。

(3) 將圖 1 中的△ACD繞點 C順時針旋轉如圖 3，連接 AE、AB、BD，∠ABD＝80°，求∠EAB的度數.

Answer 1

【答案】（1）60°；（2）180°-α，理由見解析；（3）140°

【解析】

（1）求出∠ACE=∠DCB，證出△ACE≌△DCB，根據全等性質得出∠EAC=∠BDC,再根據三角形內角和定理求出即可；（2）證出△ACE≌△DCB，根據全等性質得出∠EAC=∠BDC,再根據三角形內角和定理求出∠AFD =α，再由補角性質求出∠AFB的度數；（3）由四邊形內角和定理得出∠CAB+∠CDB=220°，再證出△ACE≌△DCB,根據全等三角形的性質得出∠CAE=∠CDB,再由周角性質求解.

解：（1）∠AFD =60°，理由如下：

如圖1，設CD與AE交于點O,

∵CA＝CD，CB＝CE，∠ACD＝∠BCE，

∴∠ACE=∠DCB,

∴△ACE≌△DCB,

∴∠EAC=∠BDC,

∵∠DOF=∠AOC, ∠DOF+∠BDC+∠AFD=∠AOC+∠EAC+∠ACD,

∴∠AFD=∠ACD=60°,

即∠AFD =60°；

（2）∠AFB=180°-α，理由如下：

如圖2，設CD與AE交于點O,

∵CA＝CD，CB＝CE，∠ACD＝∠BCE=α，

∴∠ACE=∠DCB,

∴△ACE≌△DCB,

∴∠EAC=∠BDC,

∵∠DOF=∠AOC, ∠DOF+∠BDC+∠AFD=∠AOC+∠EAC+∠ACD,

∴∠AFD=∠ACD=α,

即∠AFD =α；

∴∠AFB=180°-α

（3）∵△ACD是等邊三角形，

∴∠ACD=60°,

∵∠ABD=80°,

∴∠CAB+∠CDB=360°-60°-80°=220°,

∵∠ACD=∠BCE,

∴∠ACE=∠BCD,

∵CE=BC,AC=CD,

∴△ACE≌△DCB,

∴∠CAE=∠CDB,

∴∠CAB+∠CAE=220°,

∴∠EAB=140°.