
【題目】如圖,已知正方形ABCD邊長為1,∠EAF=45°,AE=AF,則有下列結論:
①∠1=∠2=22.5°;
②點C到EF的距離是 ![]() -1;
-1;
③△ECF的周長為2;
④BE+DF>EF.
其中正確的結論是 . (寫出所有正確結論的序號)
【答案】①②③
【解析】解:∵四邊形ABCD為正方形,
∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中![]() ,
,
∴Rt△ABE≌Rt△ADF,
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正確;
連結EF、AC,它們相交于點H,如圖,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
而AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④錯誤;
∴△ECF的周長=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2,所以③正確;
設BE=x,則EF=2x,CE=1﹣x,
∵△CEF為等腰直角三角形,
∴EF= ![]() CE,即2x=
CE,即2x= ![]() (1﹣x),解得x=
(1﹣x),解得x= ![]() ﹣1,
﹣1,
∴EF=2( ![]() ﹣1),
﹣1),
∴CH= ![]() EF=
EF= ![]() ﹣1,所以②正確.
﹣1,所以②正確.
故答案為①②③.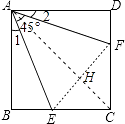
先證明Rt△ABE≌Rt△ADF得到∠1=∠2,易得∠1=∠2=∠22.5°,于是可對①進行判斷;連結EF、AC,它們相交于點H,如圖,利用Rt△ABE≌Rt△ADF得到BE=DF,則CE=CF,接著判斷AC垂直平分EF,AH平分∠EAF,于是利用角平分線的性質定理得到EB=EH,FD=FH,則可對③④進行判斷;設BE=x,則EF=2x,CE=1﹣x,利用等腰直角三角形的性質得到2x= ![]() (1﹣x),解得x=
(1﹣x),解得x= ![]() ﹣1,則可對④進行判斷.本題考查了四邊形的綜合題:熟練掌握正方形的性質和角平分線的性質定理.解決本題的關鍵是證明AC垂直平分EF.
﹣1,則可對④進行判斷.本題考查了四邊形的綜合題:熟練掌握正方形的性質和角平分線的性質定理.解決本題的關鍵是證明AC垂直平分EF.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知∠O=30°,點B是OM邊上的一個點光源,在邊ON上放一平面鏡.光線BC經
過平面鏡反射后,反射光線與邊OM的交點記為E,則△OCE是等腰三角形的個數有( )

A. 1個 B. 2個 C. 3個 D. 3個以上
查看答案和解析>>
科目:初中數學 來源: 題型:
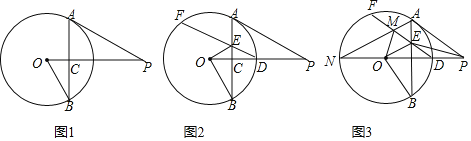
【題目】已知:PA是![]() 的切線,點B在
的切線,點B在![]() 上,連接OB,OP,連接AB交OP于點C,
上,連接OB,OP,連接AB交OP于點C,![]() .
.
![]() 如圖1,求證:
如圖1,求證:![]() ;
;
![]() 如圖2,OP交
如圖2,OP交![]() 于點D,過點D作
于點D,過點D作![]() 交AB于點E,連接OE,求證:
交AB于點E,連接OE,求證:![]() ;
;
![]() 如圖3,在
如圖3,在![]() 的條件下,延長PO交
的條件下,延長PO交![]() 于點N,連接AN交DF于點M,連接OM、EP,若
于點N,連接AN交DF于點M,連接OM、EP,若![]() ,
,![]() ,求線段BE的長.
,求線段BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形紙片ABCD中,AB=3cm,AD=5cm,折疊紙片使B點落在邊AD上的E處,折痕為PQ,過點E作EF∥AB交PQ于F,連接BF.
(1)求證:四邊形BFEP為菱形;
(2)當點E在AD邊上移動時,折痕的端點P、Q也隨之移動;
①當點Q與點C重合時(如圖2),求菱形BFEP的邊長;
②若限定P、Q分別在邊BA、BC上移動,求出點E在邊AD上移動的最大距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,∠A=140°,∠D=80°.

(1)如圖1,若∠B=∠C,試求出∠C的度數;
(2)如圖2,若∠ABC的角平分線BE交DC于點E,且BE∥AD,試求出∠C的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學校組織的游藝晚會上,擲飛鏢游戲規則如下:如圖,擲到A區和B區的得分不同,A區為小圓內部分,B區為大圓內小圓外部分(擲中一次記一個點).現統計小華、小明和小芳擲中與得分情況如圖所示,依此方法計算小芳的得分為( )

A. 76分 B. 74分 C. 72分 D. 70分
查看答案和解析>>
科目:初中數學 來源: 題型:
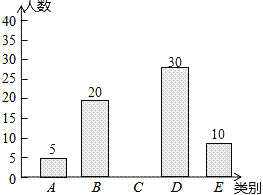
【題目】亞健康是時下社會熱門話題,進行體育鍛煉是遠離亞健康的一種重要方式,為了解某校八年級學生每天進行體育鍛煉的時間情況,隨機抽樣調查了100名初中學生,根據調查結果得到如圖所示的統計圖表.
類別 | 時間t(小時) | 人數 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
請根據圖表信息解答下列問題:
(1)a= ;
(2)補全條形統計圖;
(3)小王說:“我每天的鍛煉時間是調查所得數據的中位數”,問小王每天進行體育鍛煉的時間在什么范圍內?
(4)若把每天進行體育鍛煉的時間在1小時以上定為鍛煉達標,則被抽查學生的達標率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵市民節約用水,自來水公司特制定了新的用水收費標準,每月用水量,x(噸)與應付水費(元)的函數關系如圖.
(1)求出當月用水量不超過5噸時,y與x之間的函數關系式;
(2)某居民某月用水量為8噸,求應付的水費是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com