
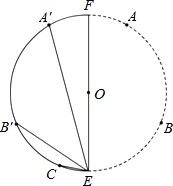
【題目】如圖,A,B,C為⊙O上相鄰的三個n等分點, ![]() ,點E在
,點E在 ![]() 上,EF為⊙O的直徑,將⊙O沿EF折疊,使點A與A′重合,點B與B′重合,連接EB′,EC,EA′.設EB′=b,EC=c,EA′=p.現探究b,c,p三者的數量關系:發現當n=3時,p=b+c.請繼續探究b,c,p三者的數量關系:當n=4時,p=;當n=12時,p= . (參考數據:sin15°=cos75°=
上,EF為⊙O的直徑,將⊙O沿EF折疊,使點A與A′重合,點B與B′重合,連接EB′,EC,EA′.設EB′=b,EC=c,EA′=p.現探究b,c,p三者的數量關系:發現當n=3時,p=b+c.請繼續探究b,c,p三者的數量關系:當n=4時,p=;當n=12時,p= . (參考數據:sin15°=cos75°= ![]() ,cos15°=sin75°=
,cos15°=sin75°= ![]() )
)
【答案】c+ ![]() b;c+
b;c+ ![]() b
b
【解析】解:如解答圖所示,連接AB、AC、BC. 由題意,點A、B、C為圓上的n等分點,
∴AB=BC,∠ACB= ![]() ×
× ![]() =
= ![]() (度).
(度).
在等腰△ABC中,過頂點B作BN⊥AC于點N,
則AC=2CN=2BCcos∠ACB=2cos ![]() BC,
BC,
∴ ![]() =2cos
=2cos ![]() .
.
連接AE、BE,在AE上取一點D,使ED=EC,連接CD.
∵∠ABC=∠CED,
∴△ABC與△CED為頂角相等的兩個等腰三角形,
∴△ABC∽△CED.
∴ ![]() ,∠ACB=∠DCE.
,∠ACB=∠DCE.
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,
∴∠ACD=∠BCE.
在△ACD與△BCE中,
∵ ![]() ,∠ACD=∠BCE,
,∠ACD=∠BCE,
∴△ACD∽△BCE.
∴ ![]() ,
,
∴DA= ![]() EB=2cos
EB=2cos ![]() EB.
EB.
∴EA=ED+DA=EC+2cos ![]() EB.
EB.
由折疊性質可知,p=EA′=EA,b=EB′=EB,c=EC.
∴p=c+2cos ![]() b.
b.
當n=4時,p=c+2cos45°b=c+ ![]() b;
b;
當n=12時,p=c+2cos15°b=c+ ![]() b.
b.
所以答案是:c+ ![]() b,c+
b,c+ ![]() b.
b.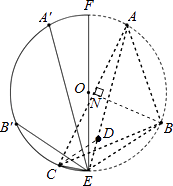


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:
【題目】在等腰△ABC中,AB=AC,∠BAC=45°,CD是△ABC的高,P是線段AC(不包括端點A,C)上一動點,以DP為一腰,D為直角頂點(D、P、E三點逆時針)作等腰直角△DPE,連接AE.

(1)如圖1,點P在運動過程中,∠EAD=______,寫出PC和AE的數量關系;
(2)如圖2,連接BE.如果AB=4,CP=![]() ,求出此時BE的長.
,求出此時BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了響應市委和市政府“綠色環保,節能減排”的號召,幸福商場用3300元購進甲、乙兩種節能燈共計100只,很快售完.這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲種節能燈 | 30 | 40 |
甲種節能燈 | 35 | 50 |
(1)求幸福商場甲、乙兩種節能燈各購進了多少只?
(2)全部售完100只節能燈后,商場共計獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,三角形的三條中線一定會交于一點,這一點就叫做三角形的重心.重心有很多美妙的性質,如關于線段比.面積比就有一些“漂亮”結論,利用這些性質可以解決三角形中的若干問題.請你利用重心的概念完成如下問題: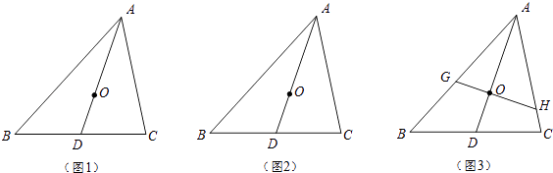
(1)若O是△ABC的重心(如圖1),連結AO并延長交BC于D,證明: ![]() ;
;
(2)若AD是△ABC的一條中線(如圖2),O是AD上一點,且滿足 ![]() ,試判斷O是△ABC的重心嗎?如果是,請證明;如果不是,請說明理由;
,試判斷O是△ABC的重心嗎?如果是,請證明;如果不是,請說明理由;
(3)若O是△ABC的重心,過O的一條直線分別與AB、AC相交于G、H(均不與△ABC的頂點重合)(如圖3),S四邊形BCHG , S△AGH分別表示四邊形BCHG和△AGH的面積,試探究 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片 ABCD 折疊,AE、EF 為折痕,點 C 落在 AD 邊上的 G 處, 并且點 B 落在 EG 邊的 H 處,若 AB=![]() ,∠BAE=30°,則 BC 邊的長為( )
,∠BAE=30°,則 BC 邊的長為( )
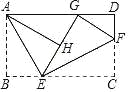
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的半徑r=25,四邊形ABCD內接于圓⊙O,AC⊥BD于點H,P為CA延長線上的一點,且∠PDA=∠ABD. 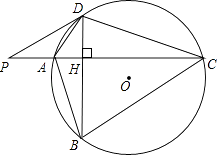
(1)試判斷PD與⊙O的位置關系,并說明理由;
(2)若tan∠ADB= ![]() ,PA=
,PA= ![]() AH,求BD的長;
AH,求BD的長;
(3)在(2)的條件下,求四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了豐富少年兒童的業余生活,某社區要在如圖所示AB所在的直線建一圖書室,本社區有兩所學校所在的位置在點C和點D處,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,試問:圖書室E應該建在距點A多少km處,才能使它到兩所學校的距離相等?

查看答案和解析>>
科目:初中數學 來源: 題型:
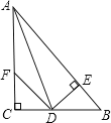
【題目】如圖:在△ABC中,∠C=90°,AD是∠BAC的平分線,DE⊥AB于E,F在AC上,BD=DF;
證明:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com