【題目】在平面直角坐標系中，直線
分別交
軸，
軸于點
.
（1）當
，自變量的取值范圍是 （直接寫出結果）；
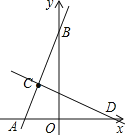
（2）點
在直線上.
①直接寫出
的值為 ；
②過
點作
交軸于點
，求直線
的解析式.
【答案】（1）
；（2）①1；② 
【解析】
（1）先利用直線y=3x+3確定A、B的解析式，然后利用一次函數的性質求解；
（2））①把C（-
，n）代入y=3x+3可求出n的值；
②利用兩直線垂直，一次項系數互為負倒數可設直線CD的解析式為y=-
x+b，然后把C（-，1）代入求出b即可．
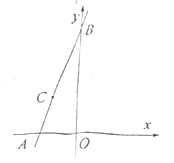
解：（1）當y=0時，3x+3=0，解得x=-1，則A（-1，0），
當x=0時，y=3x+3=3，則B（0，3），
當0＜y≤3，自變量x的取值范圍是-1≤x＜0；
（2）①把C（-，n）代入y=3x+3得3×（-）+3=n，解得n=1；
②∵AB⊥CD，
∴設直線CD的解析式為y=-x+b，
把C（-，1）代入得-×（-）+b=1，解得b=
，
∴直線CD的解析式為y=-x+．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】數軸是一個非常重要的數學工具，通過它把數和數軸上的點建立起對應關系，揭示了數與點之間的內在的聯系，它是“數形結合”的基礎，請利用數軸解決下列問題：
（1）畫出數軸，并在數軸上畫出表示下列各數的點：
（2）用“＞”號將（1）中各數連接起來；
（3）直接填空：數軸上若
點表示的數為
點表示的數為-2，則
之間的距離是 ．
（4）直接填空：若數軸上點表示的數為
，且兩點間的距離為
，則
點表示的數為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲是一個長為2a、寬為2b的長方形，沿圖中虛線用剪刀均分成四個小長方形，然后按圖乙形狀拼成一個正方形．
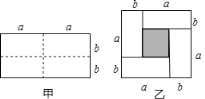
(1)你認為圖乙中陰影部分的正方形的邊長等于多少？
(2)請用兩種不同的方法求圖乙中陰影部分的面積；
(3)觀察圖乙，你能寫出 代數式(a+b)2，(a-b)2，ab之間的等量關系嗎？
(4)根據(3)題中的等量關系，解決如下問題；若
，
，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司需要粉刷一些相同的房間，經調查3名師傅一天粉刷8個房間，還剩40m2刷不完；5名徒弟一天可以粉刷9個房間；每名師傅比徒弟一天多刷30m2的墻面。
（1）求每個房間需要粉刷的面積；
（2）該公司現有36個這樣的房間需要粉刷，若只聘請1名師傅和2名徒弟一起粉刷，需要幾天完成？
（3）若來該公司應聘的有3名師傅和10名徒弟，每名師傅和每名徒弟每天的工資分別是240元和200元，該公司要求這36個房間要在2天內粉刷完成，問人工費最低是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
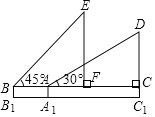
【題目】如圖是小紅在一次放風箏活動中某時段的示意圖，她在A處時的風箏線（整個過程中風箏線近似地看作直線）與水平線構成30°角，線段AA1表示小紅身高1.5米．
（1）當風箏的水平距離AC=18米時，求此時風箏線AD的長度；
（2）當她從點A跑動9
米到達點B處時，風箏線與水平線構成45°角，此時風箏到達點E處，風箏的水平移動距離CF=10
米，這一過程中風箏線的長度保持不變，求風箏原來的高度C1D．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用“※”定義一種新運算：對于任意有理數a和b，規定a※b＝ab2+2ab+a．
如：1※2＝1×22+2×1×2+1＝9
（1）（﹣2）※3＝ ；
（2）若
※3＝16，求a的值；
（3）若2※x＝m，（
x）※3＝n（其中x為有理數），試比較m，n的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】六盤水市梅花山國際滑雪自建成以來，吸引大批滑雪愛好者，一滑雪者從山坡滑下，測得滑行距離y（單位：cm）與滑行時間x（單位：s）之間的關系可以近似的用二次函數來表示．
滑行時間x/s | 0 | 1 | 2 | 3 | … |
滑行距離y/cm | 0 | 4 | 12 | 24 | … |
（1）根據表中數據求出二次函數的表達式．現測量出滑雪者的出發點與終點的距離大約800m，他需要多少時間才能到達終點？
（2）將得到的二次函數圖象補充完整后，向左平移2個單位，再向上平移5個單位，求平移后的函數表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知關于x的一元二次方程x2+2x+
=0有兩個不相等的實數根，k為正整數.
（1）求k的值；
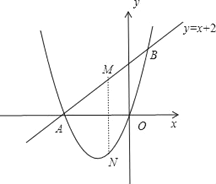
（2）當此方程有一根為零時，直線y=x+2與關于x的二次函數y=x2+2x+的圖象交于A、B兩點，若M是線段AB上的一個動點，過點M作MN⊥x軸，交二次函數的圖象于點N，求線段MN的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是放在地面上的一個長方體盒子，其中
，在線段
的三等分點
（
E=3）處有一只螞蟻，
中點
處有一米粒，則螞蟻沿長方體表面爬到米粒處的最短距離為（ ）
A.10
B.
C.5+
D.6+
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com