【題目】已知：二次函數y=x2+bx+c的圖象與x軸交于A，B兩點，其中A點坐標為（﹣3，0），與y軸交于點C，點D（﹣2，﹣3）在拋物線上． 
（1）求拋物線的解析式；
（2）拋物線的對稱軸上有一動點P，求出PA+PD的最小值；
（3）若拋物線上有一動點P，使三角形ABP的面積為6，求P點坐標．
【答案】
（1）解：因為二次函數y=x2+bx+c的圖象經過A（﹣3，0），D（﹣2，﹣3），所以 
，
解得 
．
所以一次函數解析式為y=x2+2x﹣3
（2）解：∵拋物線對稱軸x=﹣1，D（﹣2，﹣3），C（0，﹣3），
∴C、D關于x軸對稱，連接AC與對稱軸的交點就是點P，
此時PA+PD=PA+PC=AC= 
= 
=3 
（3）解：設點P坐標（m，m2+2m﹣3），
令y=0，x2+2x﹣3=0，
x=﹣3或1，
∴點B坐標（1，0），
∴AB=4
∵S△PAB=6，
∴ 
4|m2+2m﹣3|=6，
∴m2+2m﹣6=0，m2+2m=0，
∴m=0或﹣2或1+ 
或1﹣ ．
∴點P坐標為（0，﹣3）或（﹣2，﹣3）或（1+ ，3）或（1﹣ ，3）．
【解析】（1）把A、D兩點坐標代入二次函數y=x2+bx+c，解方程組即可解決．（2）利用軸對稱找到點P，用勾股定理即可解決．（3）根據三角形面積公式，列出方程即可解決．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，過邊長為1的等邊△ABC的邊AB上一點P，作PE⊥AC于E，Q為BC延長線上一點，當PA=CQ時，連PQ交AC邊于D，則DE的長為( )
A. 
B. 
C. 
D. 不能確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】縣城
路公交車每隔一定時間發車一次，一天小明在街上勻速行走，發現背后每隔
分鐘開過來一輛公交車，而迎面每隔
分鐘有一輛公交車駛來，則公交車每隔________分鐘發車一次．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀對學生的成長有著深遠的影響，某中學為了解學生每周課余閱讀的時間，在本校隨機抽取了若干名學生進行調查，并依據調查結果繪制了以下不完整的統計圖表．
組別 | 時間（小時） | 頻數（人數） | 頻率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合計 | 1 |
請根據圖表中的信息，解答下列問題：
（1）表中的a= ，b= ，中位數落在 組，將頻數分布直方圖補全；
（2）估計該校2000名學生中，每周課余閱讀時間不足0.5小時的學生大約有多少名？
（3）E組的4人中，有1名男生和3名女生，該校計劃在E組學生中隨機選出兩人向全校同學作讀書心得報告，請用畫樹狀圖或列表法求抽取的兩名學生剛好是1名男生和1名女生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
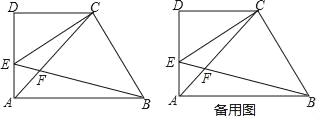
【題目】已知：如圖，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，點E在邊AD上（不與點A、D重合），∠CEB=45°，EB與對角線AC相交于點F，設DE=x．
（1）用含x的代數式表示線段CF的長；
（2）如果把△CAE的周長記作C△CAE，△BAF的周長記作C△BAF，設
=y，求y關于x的函數關系式，并寫出它的定義域；
（3）當∠ABE的正切值是
時，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB=AD，那么添加下列一個條件后，仍無法判定△ABC≌△ADC的是（ ）
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
