
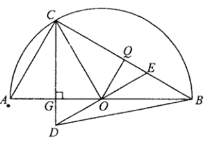
【題目】如圖1,以![]() 為直徑作半圓
為直徑作半圓![]() ,點
,點![]() 在半圓上,連結
在半圓上,連結![]() ,
,![]() ,且
,且![]() .連結
.連結![]() ,
,![]() 是
是![]() 邊上的高,過點
邊上的高,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,交
,交![]() 于點
于點![]() .
.
(1)求證:![]() .
.
(2)當![]() 為
為![]() 的中點時,求
的中點時,求![]() 的值.
的值.
(3)如圖2,取![]() 的中點
的中點![]() ,連結
,連結![]() .
.
①若![]() ,在點
,在點![]() 運動過程中,當四邊形
運動過程中,當四邊形![]() 的其中一邊長是
的其中一邊長是![]() 的2倍時,求所有滿足條件的
的2倍時,求所有滿足條件的![]() 長.
長.
②連結![]() ,當
,當![]() 的面積是
的面積是![]() 的面積的3倍時,求
的面積的3倍時,求![]() 的值(請直接寫出答案).
的值(請直接寫出答案).
圖1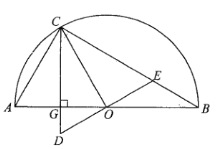 圖2
圖2
【答案】(1)見解析;(2)![]() ;(3)①當
;(3)①當![]() 或
或![]() 時,四邊形
時,四邊形![]() 其中一邊長為
其中一邊長為![]() 的2倍;②
的2倍;②![]()
【解析】
(1)先證明![]() 再證明
再證明![]() ,從而可得結論;
,從而可得結論;
(2)先證明![]() 是等邊三角形,再證明
是等邊三角形,再證明![]() ,利用銳角三角函數可得結論;(3)①分情況討論:i當
,利用銳角三角函數可得結論;(3)①分情況討論:i當![]() ,ii當
,ii當![]() ,iii當
,iii當![]() ,結合圖形性質可得結論;②當
,結合圖形性質可得結論;②當![]() 的面積是
的面積是![]() 的面積的3倍時,得到
的面積的3倍時,得到![]() 設
設![]() 則
則 ![]() 結合圖形的性質用含
結合圖形的性質用含![]() 的代數式表示
的代數式表示![]() 利用正切的定義可得答案.
利用正切的定義可得答案.
解:(1)∵![]() ,
,
∴![]() .
.
∵![]() 為
為![]() 的直徑,
的直徑,
∴![]() ,且
,且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
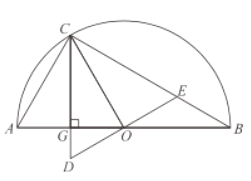
(2)∵![]() 為
為![]() 邊上的高,且
邊上的高,且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
又∵![]() 為
為![]() 中點,且
中點,且![]() ,
,
∴![]() .
.
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() .
.
∵![]() .
.
![]()
![]() ,
,
∴![]()
(3)①i當![]() ,由題意得:
,由題意得:
設![]() 為
為![]() ,則
,則![]()
∴![]()
由![]() ,得
,得![]()
∴![]() .
.
由![]()
得![]() .
.
∴![]()
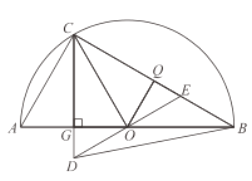
ii當![]()
設![]() 為
為![]() ,則
,則![]() .
.
由![]() 得,
得,
![]() ,化簡
,化簡![]() ,
,
![]() ,
,![]() (舍)
(舍)
∴![]()
iii當![]()
由于![]() ,且
,且![]()
∴不存在
綜上所述,當![]() 或
或![]() 時,四邊形
時,四邊形![]() 其中一邊長為
其中一邊長為![]() 的2倍.
的2倍.
②如圖,當![]() 的面積是
的面積是![]() 的面積的3倍時,
的面積的3倍時,
![]()
設![]() 則
則 ![]()
![]()
![]() 為
為![]() 的中點,
的中點,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
設![]() 則
則![]()
![]()
![]()
解得:![]() 或
或![]() 舍去,
舍去,
![]()
![]()
![]()
同理可得:![]()
![]()
![]()
![]()
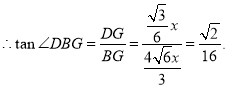


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:
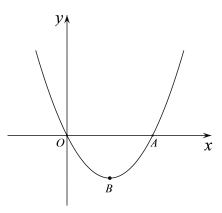
【題目】如圖,拋物線y=x2+mx(m<0)交x軸于O,A兩點,頂點為點B.
(1)求△AOB的面積(用含m的代數式表示);
(2)直線y=kx+b(k>0)過點B,且與拋物線交于另一點D(點D與點A不重合),交y軸于點C.過點C作CE∥AB交x軸于點E.
(ⅰ) 若∠OBA=90°,2<![]() <3,求k的取值范圍;
<3,求k的取值范圍;
(ⅱ) 求證:DE∥y軸.
查看答案和解析>>
科目:初中數學 來源: 題型:
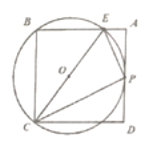
【題目】如圖,已知在正方形![]() 中,
中,![]() ,
,![]() 是線段
是線段![]() 上的一動點,連接
上的一動點,連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() .以
.以![]() 為直徑作
為直徑作![]() ,當點
,當點![]() 從點
從點![]() 移動到點
移動到點![]() 時,對應點
時,對應點![]() 也隨之運動,則點
也隨之運動,則點![]() 運動的路程長度為____________.
運動的路程長度為____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 及一次函數
及一次函數![]() ,將該二次函數在
,將該二次函數在![]() 軸上方的圖象沿
軸上方的圖象沿![]() 軸翻折到
軸翻折到![]() 軸下方,圖象的其余部分不變,得到一個新函數的圖象(如圖所示),當直線
軸下方,圖象的其余部分不變,得到一個新函數的圖象(如圖所示),當直線![]() 與新函數圖象有4個交點時,
與新函數圖象有4個交點時,![]() 的取值范圍是( )
的取值范圍是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() (點
(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,頂點為
,頂點為![]() .
.
(Ⅰ)當![]() 時,求二次函數的最大值;
時,求二次函數的最大值;
(Ⅱ)當![]() 時,點
時,點![]() 是
是![]() 軸上的點,
軸上的點,![]() ,將點
,將點![]() 繞點
繞點![]() 順時針旋轉90°得到點
順時針旋轉90°得到點![]() ,點
,點![]() 恰好落在該二次函數的圖象上,求
恰好落在該二次函數的圖象上,求![]() 的值;
的值;
(Ⅲ)![]() 是該二次函數圖象上的一點,在(Ⅱ)的條件下,連接
是該二次函數圖象上的一點,在(Ⅱ)的條件下,連接![]() ,
,![]() ,使
,使![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
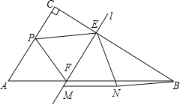
【題目】如圖,Rt![]() ABC中,∠C=90°,AC=10,BC=16.動點P以每秒3個單位的速度從點A開始向點C移動,直線l從與AC重合的位置開始,以相同的速度沿CB方向平行移動,且分別與CB,AB邊交于E,F兩點,點P與直線l同時出發,設運動的時間為t秒,當點P移動到與點C重合時,點P和直線l同時停止運動.在移動過程中,將
ABC中,∠C=90°,AC=10,BC=16.動點P以每秒3個單位的速度從點A開始向點C移動,直線l從與AC重合的位置開始,以相同的速度沿CB方向平行移動,且分別與CB,AB邊交于E,F兩點,點P與直線l同時出發,設運動的時間為t秒,當點P移動到與點C重合時,點P和直線l同時停止運動.在移動過程中,將![]() PEF繞點E逆時針旋轉,使得點P的對應點M落在直線l上,點F的對應點記為點N,連接BN,當BN∥PE時,t的值為_____.
PEF繞點E逆時針旋轉,使得點P的對應點M落在直線l上,點F的對應點記為點N,連接BN,當BN∥PE時,t的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點A坐標為![]() ,點B的坐標為
,點B的坐標為![]() .將二次函數
.將二次函數![]() 的圖象經過左(右)平移
的圖象經過左(右)平移![]() 個單位再上(下)平移
個單位再上(下)平移![]() 個單位得到圖象M,使得圖象M的頂點落在線段AB上.下列關于a,b的取值范圍,敘述正確的是( )
個單位得到圖象M,使得圖象M的頂點落在線段AB上.下列關于a,b的取值范圍,敘述正確的是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個四位數,記千位數字與個位數字之和為![]() ,十位數字與百位數字之和為
,十位數字與百位數字之和為![]() ,如果
,如果![]() ,那么稱這個四位數為“對稱數”
,那么稱這個四位數為“對稱數”
![]() 最小的“對稱數”為 ;四位數
最小的“對稱數”為 ;四位數![]() 與
與![]() 之和為最大的“對稱數”,則
之和為最大的“對稱數”,則![]() 的值為 ;
的值為 ;
![]() 一個四位的“對稱數”
一個四位的“對稱數”![]() ,它的百位數字是千位數字
,它的百位數字是千位數字![]() 的
的![]() 倍,個位數字與十位數字之和為
倍,個位數字與十位數字之和為![]() ,且千位數字
,且千位數字![]() 使得不等式組
使得不等式組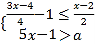 恰有
恰有![]() 個整數解,求出所有滿足條件的“對稱數”
個整數解,求出所有滿足條件的“對稱數”![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com