
【題目】已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
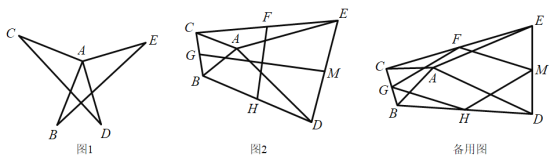
(1)觀察猜想
如圖1,當![]() 時,請直接寫出線段
時,請直接寫出線段![]() 與
與![]() 的數量關系: ;位置關系: ;
的數量關系: ;位置關系: ;
(2)類比探究
如圖2,已知![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() ,
,![]() 的中點,寫出
的中點,寫出![]() 與
與![]() 的數量關系和位置關系,并說明理由;
的數量關系和位置關系,并說明理由;
(3)解決問題
如圖,已知:![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() ,
,![]() ,
,![]() 的中點,將
的中點,將![]() 繞點
繞點![]() 旋轉,直接寫出四邊形
旋轉,直接寫出四邊形![]() 的面積
的面積![]() 的范圍(用含
的范圍(用含![]() 的三角函數式子表示).
的三角函數式子表示).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,理由見解析;(3)
,理由見解析;(3)![]() .
.
【解析】
(1)利用三角形全等三角形或圖形旋轉的性質問題可解;
(2)在(1)中結論的基礎上,利用三角形中位線的性質證明四邊形![]() 是菱形,證明
是菱形,證明![]() ,利用銳角三角函數的知識可證明
,利用銳角三角函數的知識可證明![]() ;
;
(3)在(2)的基礎上,證明四邊形![]() 是菱形,利用中位線性質證明到菱形的邊GF是CD的一半,通過旋轉的過程得到CD的取值范圍,再利用三角函數的知識,表示菱形
是菱形,利用中位線性質證明到菱形的邊GF是CD的一半,通過旋轉的過程得到CD的取值范圍,再利用三角函數的知識,表示菱形![]() 面積,則問題可解.
面積,則問題可解.
(1)如圖
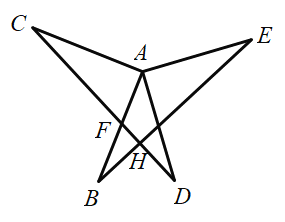
∵![]()
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,![]() =
=![]()
∵![]()
∴![]()
故答案為:![]() ,
,![]()
(2)![]() ,
,![]() .
.
理由如下:
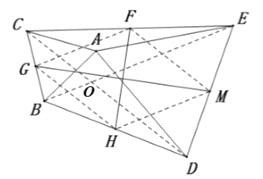
連接![]() ,
,![]() ,
,
![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
連接![]() ,
,
∵![]() 分別是
分別是![]() 的中點,
的中點,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴四邊形![]() 是菱形,
是菱形,
∴![]()
∵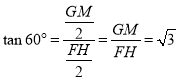 ,
,
∴![]() .
.
(3)![]()
如圖,
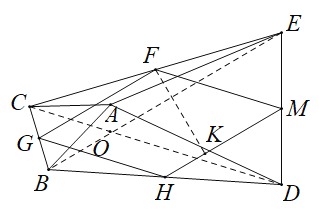
由(2)同理可知,四邊形![]() 是菱形,
是菱形,![]() ,
,
將![]() 繞點
繞點![]() 旋轉過程中,
旋轉過程中,![]()
則菱形![]() 的邊長GF范圍為
的邊長GF范圍為![]()
過F做![]() 于K
于K
菱形的面積為![]()
寫出四邊形![]() 的面積
的面積![]() 的范圍為:
的范圍為:![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩個種子店都銷售“黃金1號”玉米種子.在甲店,該種子的價格為 5元 / kg,如果一次購買2 kg 以上的種子,超過 2 kg 部分的種子的價格打8折.在乙店,不論一次購買該種子的數量是多少,價格均為4.5 元 / kg.
(1)根據題意,填寫下表:

(2)設一次購買種子的數量為![]() kg(
kg(![]() ). 在甲店購買的付款金額記為
). 在甲店購買的付款金額記為![]() 元,在乙店購買的付款金額為
元,在乙店購買的付款金額為![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3) 若在同一店中一次購買種子的付款金額是36元,則最多可購買種子______ kg.若在同一店中一次購買種子10 kg,則最少付款金額是________元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 的網格中,
的網格中,![]() 均在格點上,請用無刻度的直尺作圖(保留作圖痕跡,不寫作法).
均在格點上,請用無刻度的直尺作圖(保留作圖痕跡,不寫作法).
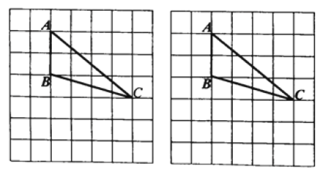
(1)在圖1中找一格點![]() ,使得
,使得![]() 為等腰三角形(找到一個即可);
為等腰三角形(找到一個即可);
(2)在圖2中作出![]() 的角平分線.
的角平分線.
查看答案和解析>>
科目:初中數學 來源: 題型:
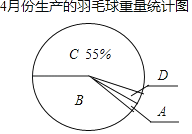
【題目】一只羽毛球的重量合格標準是5.0克~5.2克(含5.0克,不含5.2克),某廠對4月份生產的羽毛球重量進行抽樣檢驗.并將所得數據繪制成如圖統計圖表.
4月份生產的羽毛球重量統計表
組別 | 重量x(克) | 數量(只) |
A | x<5.0 | m |
B | 5.0≤x<5.1 | 400 |
C | 5.1≤x<5.2 | 550 |
D | x≥5.2 | 30 |
(1)求表中m的值及圖中B組扇形的圓心角的度數.
(2)問這些抽樣檢驗的羽毛球中,合格率是多少?如果購得4月份生產的羽毛球10筒(每筒12只),估計所購得的羽毛球中,非合格品的羽毛球有多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
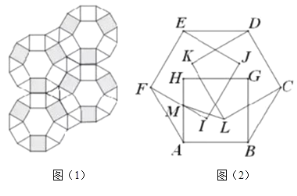
【題目】建筑工人用邊長相等的正六邊形、正方形、正三角形三種瓷磚鋪設地面,正方形瓷磚分黑白兩種顏色,密鋪成圖(1)的形狀.用水泥澆筑前,為方便施工,工人要先把瓷磚按圖1方式先擺放好,一工人擺放時,無意間將3塊黑色正方形瓷磚上翻到一個正六邊形的上面,其中三個正方形的一條邊分別和正六邊形的三條邊重合,如圖(2)所示.按圖(2)方式給各點作上標注,若正方形的邊長![]() ,則
,則![]() _____
_____![]() (不考慮瓷磚的厚度)
(不考慮瓷磚的厚度)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據報載,在“百萬家庭低碳行,垃圾分類要先行”活動中,某地區對隨機抽取的1000名公民的年齡段分布情況和對垃圾分類所持態度進行調查,并將調查結果分別繪成條形圖(圖1)、扇形圖(圖2).
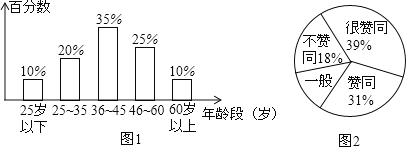
(1)圖2中所缺少的百分數是_________;
(2)這次隨機調查中,如果公民年齡的中位數是正整數,那么這個中位數所在年齡段是_________(填寫年齡段);
(3)這次隨機調查中,年齡段是“25歲以下”的公民中“不贊成”的有5名,它占“25歲以下”人數的百分數是________;
(4)如果把所持態度中的“很贊同”和“贊同”統稱為“支持”,那么這次被調查公民中“支持”的人有_______名.
查看答案和解析>>
科目:初中數學 來源: 題型:
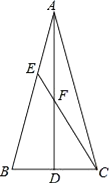
【題目】如圖,在△ABC中,∠BAC=30°,AB=AC,AD是BC邊上的中線,∠ACE=![]() ∠BAC,CE交AB于點E,交AD于點F.若BC=2,則EF的長為__.
∠BAC,CE交AB于點E,交AD于點F.若BC=2,則EF的長為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實現2020年全面脫貧的目標,我國實施“精準扶貧”戰略,從而使貧困戶的生活條件得到改善,生活質量明顯提高.為了切實關注、關愛貧困家庭學生,某校對全校各班貧困家庭學生的人數情況進行了統計,統計發現班上貧困家庭學生人數分別有2名,3名,4名,5名,6名,共五種情況.并將其制成了如下兩幅不完整的統計圖:

請回答下列問題:
(1)求該校一共有班級________個;在扇形統計圖中,貧困家庭學生人數有5名的班級所對應扇形圓心角為________°;
(2)將條形圖補充完整;
(3)甲、乙、丙是貧困生中的三名學生,學校決定從這三名學生中隨機抽取兩名代表到市里進行發言,用列表法或畫樹狀圖法,求同時抽到甲,乙兩名學生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com