【題目】甲、乙兩輛汽車分別在相距180千米的A、B兩地相向而行，甲車每小時比乙車每小時快20千米，甲車在乙車出發2小時后出發，甲車出發1小時兩車相遇。
（1）求甲、乙兩車的速度各是多少？
（2）甲、乙兩車各自到達目的地后都立即返回，問甲車從A地出發多長時間甲、乙兩車 相距20千米？
【答案】（1）甲車速度為60 km/h，乙車速度為40km/h；（2）甲車從A地出發4.4小時或4.8小時甲、乙兩車相距20千米.
【解析】
（1）設乙車速度是x km/h，甲車速度是x+20 km/h.根據甲車行駛的路程+乙車行駛的路程=180.列出方程解方程即可；
（2）設甲車從A地出發y小時甲、乙兩車相距20千米.分兩種情況①甲乙返回時相遇之前，則有甲車行駛的路程+乙車行駛的路程+20=總路程的三倍.②甲乙返回時相遇之后，則有甲車行駛的路程+乙車行駛的路程=總路程的三倍+20.根據等量關系列出方程即可.
解：（1）設乙車速度是x km/h，甲車速度是x+20 km/h.根據題意
解得x=40，則x+20=60
所以甲車速度為60 km/h，乙車速度為40km/h.
（2）設甲車從A地出發y小時甲、乙兩車相距20千米.
根據題意可分兩種情況討論
①甲乙兩車返回后還沒相遇，則
解得
②甲乙兩車返回后相遇后，距離20km
解得
故甲車從A地出發4.4小時或4.8小時甲、乙兩車相距20千米.
科目：初中數學 來源： 題型：
【題目】如圖，E為矩形ABCD的邊AB上一點，將矩形沿CE折疊，使點B恰好落在ED上的點F處，若BE=1，BC=3，則CD的長為（ ）
A.5B.6C.4D.3
查看答案和解析>>
科目：初中數學 來源： 題型：
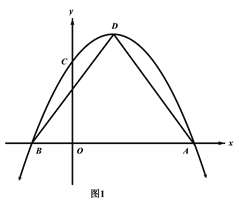
【題目】如圖1，拋物線
與x軸相交于A，B兩點（點A在點B的右側），與y軸交于點C，點D是拋物線的頂點，連接AD、BD.
求△ABD的面積；
如圖2，連接AC、BC，若點P是直線AC上方拋物線上一動點，過P作PE//BC交AC于點E，作PQ//y軸交AC于點Q，當△PQE周長最大時，將△PQE沿著直線AC平移，記移動中的△PQE為
，連接
，求△PQE的周長的最大值及
的最小值；
如圖3，點G為x軸正半軸上一點，且OG=OC，連接CG，過G作GH⊥AC于點H，將△CGH繞點O順時針旋轉
（
），記旋轉中的△CGH為
，在旋轉過程中，直線
,
分別與直線AC交于點M，N， 
能否成為等腰三角形？若能直接寫出所有滿足條件的
的值；若不能，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的個數是（ ）
（1）若
，則
（2）若
，則
（3）若
，則
（4）若兩個角互補，則這兩個角是鄰補角
（5）有公共頂點且有一條公共邊的兩個角是鄰補角
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】Rt△ABC中，∠ACB＝90°，AC:BC＝4:3，O是BC上一點，⊙O交AB于點D，交BC延長線于點E．連接ED，交AC于點G，且AG＝AD．
（1）求證：AB與⊙O相切；
（2）設⊙O與AC的延長線交于點F，連接EF，若EF∥AB，且EF＝5，求BD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩個車間接到加工一批零件的任務，從開始加工到完成這項任務共用了9天．其間，乙車間在加工2天后停止加工，引入新設備后繼續加工，直到與甲車間同時完成這項任務為止，設甲、乙兩個車間各自加工零件總數y（單位：件）與加時間x（單位：天）的對應關系如圖1所示，由工廠統計數據可知，甲車間與乙車間加工零件總數之差z（單位：件）與加時間x（單位：天）的對應關系如圖2所示，請根據圖象提供的信息回答：
圖中
的值是__________；
第_________天時，甲、乙兩個車間加工零件總數相同.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，⊙O是△ABC的外接圓，BC為⊙O的直徑，點E為△ABC的內心，連接AE并延長交⊙O于D點，連接BD并延長至F，使得BD
DF，連接CF、BE．
（1）求證：DBDE；
（2）求證：直線CF為⊙O的切線；
（3）若CF4，求圖中陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
