
【題目】如圖,在![]() 中,
中,![]()
![]() 是斜邊
是斜邊![]() 上兩點,且
上兩點,且![]() 將
將![]() 繞點
繞點![]() 順時針旋轉90°后,得到
順時針旋轉90°后,得到![]() 連接
連接![]()
(1)求證: △AED≌△AEF
(2)猜想線段BE,ED,DC之間的關系,并證明
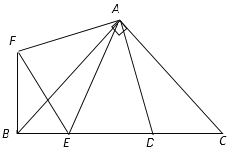
【答案】(1)見解析 (2)![]() ,證明見解析
,證明見解析
【解析】
(1)由旋轉的性質可得:AD=AF,∠BAC=∠FAD=90°,由![]() 可得∠FAE=
可得∠FAE=![]() ,所以
,所以![]() ,又AE=AE,故可證△AED≌△AEF
,又AE=AE,故可證△AED≌△AEF
(2)由旋轉的性質可得:BF=CD,∠ACB=∠ABF,可證∠FBE=90°,由(1)可得:EF=ED,根據勾股定理可得:![]() ,故可得
,故可得![]()
∵△ADC繞點A順時針旋轉90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,
∴AD=AF,
∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°,
∴∠DAE=∠FAE,
∵在△AED與△AEF中,
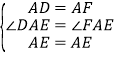
∴△AED≌△AEF(SAS)
(2)∵△AED≌△AEF,
∴ED=FE,∠ACB=∠ABF,
在Rt△ABC中,
∵∠ABC+∠ACB=90°,
∴∠ABC+∠ABF=90°即∠FBE=90°,
∴BE2+BF2=FE2,即BE2+DC2=DE2


 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:初中數學 來源: 題型:
【題目】某中學數學興趣小組為了解本校學生對電視節目的喜愛情況,隨機調查了部分學生最喜愛哪一類節目 (被調查的學生只選一類并且沒有不選擇的),并將調查結果制成了如下的兩個統計圖(不完整).請你根據圖中所提供的信息,完成下列問題:
(1)求本次調查的學生人數;
(2)請將兩個統計圖補充完整,并求出新聞節目在扇形統計圖中所占圓心角的度數;
(3)若該中學有2000名學生,請估計該校喜愛電視劇節目的人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖.在Rt△ABC中,∠A=90°,AB=AC=4.點E為Rt△ABC邊上一點,以每秒1單位的速度從點C出發,沿著C→A→B的路徑運動到點B為止.連接CE,以點C為圓心,CE長為半徑作⊙C,⊙C與線段BC交于點D.設扇形DCE面積為S,點E的運動時間為t.則在以下四個函數圖象中,最符合扇形面積S關于運動時間t的變化趨勢的是( )

A. 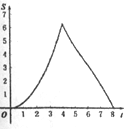 B.
B. 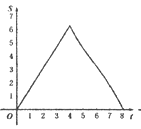
C. 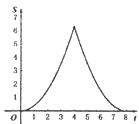 D.
D. 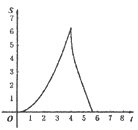
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:正方形ABCD中,∠MAN=45°,∠MAN繞點A順時針旋轉,它的兩邊分別交CB,DC(或它們的延長線)于點M,N.當∠MAN繞點A旋轉到BM=DN時(如圖1),易證BM+DN=MN.

(1)當∠MAN繞點A旋轉到BM≠DN時(如圖2),線段BM,DN和MN之間有怎樣的數量關系?寫出猜想,并加以證明.
(2)當∠MAN繞點A旋轉到如圖3的位置時,線段BM,DN和MN之間又有怎樣的數量關系?請直接寫出你的猜想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在網上銷售蘋果,原計劃每天賣100斤,但實際每天的銷量與計劃銷量相比有出入,如表是某周7天的銷售情況(超額記為正,不足記為負.單位:斤):

(1)根據記錄的數據可知銷售量最多的一天比銷售量最少的一天多銷售 斤;
(2)本周實際銷售總量達到了計劃銷量沒有?
(3)若每斤按5元出售,每斤蘋果的運費為1元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l1∥l2∥l3∥l4,相鄰兩條平行線間的距離都是1,正方形ABCD的四個頂點分別在四條直線上,則正方形ABCD的面積為( )

A. ![]() B.
B. ![]() C. 3 D. 5
C. 3 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
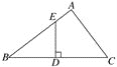
【題目】已知,如圖,在△ABC中,D是BC的中點,DE⊥BC,垂足為D,交AB于點E,且BE2-EA2=AC2,
(1)求證:∠A=90°.
(2)若DE=3,BD=4,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 的中點,點
的中點,點![]() 從
從![]() 點出發,先以每秒
點出發,先以每秒![]() 的速度運動到
的速度運動到![]() ,然后以每秒
,然后以每秒![]() 的速度從
的速度從![]() 運動到
運動到![]() .當點
.當點![]() 運動時間
運動時間![]() _______秒時,三角形
_______秒時,三角形![]() 的面積為
的面積為![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com