
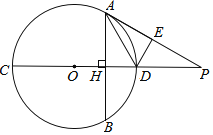
【題目】如圖,CD為⊙O的直徑,弦AB垂直于CD,垂足為H,∠EAD=∠HAD.
(1)求證:AE為⊙O的切線;
(2)延長AE與CD的延長線交于點P,過D 作DE⊥AP,垂足為E,已知PA=2,PD=1,求⊙O的半徑和DE的長.
【答案】(1)見解析;(2)1.5,DE=![]()
【解析】
(1)連接OA,根據垂線的定義結合角的計算,即可得出∠EAD+∠OAD=90°,從而得出OA⊥AE,再由點A在圓上,即可證出AE為⊙O的切線;
(2)設⊙O的半徑為x,在Rt△AOP中,利用勾股定理可求出x的值,再由DE⊥AP,得出OA∥DE,進而可得出△PED∽△PAO,根據相似三角形的性質即可求出DE的長度.
(1)證明:連結OA,如圖所示.
∵AB⊥CD,
∴∠AHD=90°,
∴∠HAD+∠ODA=90°.
∵OA=OD,
∴∠OAD=∠ODA.
又∵∠EAD=∠HAD,
∴∠EAD+∠OAD=90°,
∴OA⊥AE.
又∵點A在圓上,
∵AE為⊙O的切線.
(2)解:設⊙O的半徑為x,在Rt△AOP中,
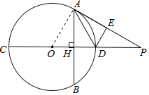
OA2+AP2=OP2,即x2+22=(x+1)2,
解得:x=1.5,
∴⊙O的半徑為1.5.
∵DE⊥AP,OA⊥AP,
∴OA∥DE,
∴△PED∽△PAO,
∴![]() ,即
,即![]() ,
,
解得:DE=![]() .
.


 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
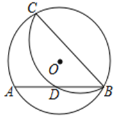
【題目】如圖, 在⊙O 中,點 C 在優弧 AB 上, 將弧 BC 沿 BC 折疊后剛好經過 AB的中點 D. 若⊙O的半徑為![]() ,AB=4,則 BC 的長是( )
,AB=4,則 BC 的長是( )
A.2![]() B.3
B.3![]() C.4D.2
C.4D.2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】垃圾分類是必須要落實的國家政策,環衛部門要求垃圾要按![]() 可回收物,
可回收物,![]() 有害垃圾,
有害垃圾,![]() 餐廚垃圾,
餐廚垃圾,![]() 其它垃圾四類分別裝袋,投放.甲投放了一袋垃圾,乙投放了兩袋垃圾(兩袋垃圾不同類).
其它垃圾四類分別裝袋,投放.甲投放了一袋垃圾,乙投放了兩袋垃圾(兩袋垃圾不同類).
(1)直接寫出甲投放的垃圾恰好是![]() 類垃圾的概率;
類垃圾的概率;
(2)用樹狀圖求乙投放的垃圾恰有一袋與甲投放的垃圾是同類的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
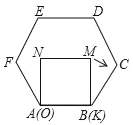
【題目】已知正方形MNOK和正六邊形ABCDEF邊長均為2,把正方形放在正六邊形中,使OK邊與AB邊重合,如圖所示,按下列步驟操作:將正方形在正六邊形中繞點B順時針旋轉,使KM邊與BC邊重合,完成第一次旋轉;再繞點C順時針旋轉,使MN邊與CD邊重合,完成第二次旋轉;…在這樣連續6次旋轉的過程中,點B,M之間距離的最小值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】文明交流互鑒是推動人類文明進步和世界和平發展的重要動力.2019年5月“ 亞洲文明對話大會”在北京成功舉辦,引起了世界人民的極大關注.某市一研究機構為了了解10~60歲年齡段市民對本次大會的關注程度,隨機選取了100名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
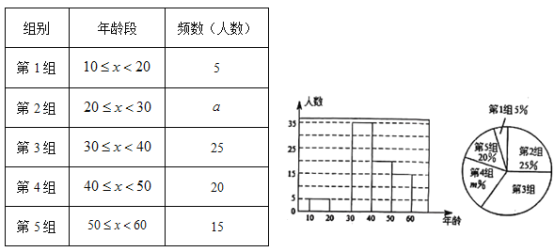
(1)請直接寫出![]() _______,
_______,![]() _______,第3組人數在扇形統計圖中所對應的圓心角是_______度.
_______,第3組人數在扇形統計圖中所對應的圓心角是_______度.
(2)請補全上面的頻數分布直方圖.
(3)假設該市現有10~60歲的市民300萬人,問40~50歲年齡段的關注本次大會的人數約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,點E,F分別是邊BC,AB上的點,且CE=BF,連接DE,過點E作EG⊥DE,使EG=DE,連接FG,FC.

(1)請判斷:FG與CE的數量關系是__________,位置關系是__________;
(2)如圖2,若點E、F分別是CB、BA延長線上的點,其它條件不變,(1)中結論是否仍然成立?請出判斷判斷并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:已知點![]() 是三角形邊上的一點(頂點除外),若它到三角形一條邊的距離等于它到三角形的一個頂點的距離,則我們把點
是三角形邊上的一點(頂點除外),若它到三角形一條邊的距離等于它到三角形的一個頂點的距離,則我們把點![]() 叫做該三角形的等距點.
叫做該三角形的等距點.
(1)如圖1:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在斜邊
在斜邊![]() 上,且點
上,且點![]() 是
是![]() 的等距點,試求
的等距點,試求![]() 的長;
的長;
(2)如圖2,![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,
上,![]() ,
,![]() 為
為![]() 中點,且
中點,且![]() .
.
①求證:![]() 的外接圓圓心是
的外接圓圓心是![]() 的等距點;②求
的等距點;②求![]() 的值.
的值.
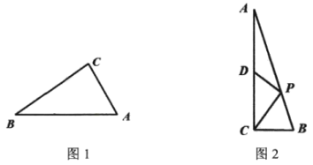
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將直線y=x向下平移b個單位長度后得到直線l,l與反比例函數y=![]() (k>0,x>0)的圖象相交于點A,與x軸相交于點B,若OA2﹣OB2=20,則k的值是( )
(k>0,x>0)的圖象相交于點A,與x軸相交于點B,若OA2﹣OB2=20,則k的值是( )
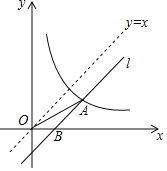
A.15B.5C.20D.10
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com